Checking for Leap Years
- MF: Again, I'm wanting us to be mindful of mathematical level here. Divisibility might not be a comfortable topic for our NYC students... And there are a lot of different constraints with this leap year issue.
- MF: The last question here ("Which script is the most beatuiful?") is a tricky one. In a CS10 class, students might be comfortable with the subjectivity of this question based on their classroom culture, but I would think most high school math or computer sceince students are going to be expecting questions to have a "right answer" and if we want to ask questions like this, we might need to be careful to help teachers build a culture that is more comfortable with questions like this.
Some years in our (Gregorian) calendar are "leap years." In a leap year, February has a 29th day and the year overall has 366. Leap years let the calendar adjust for the fact that it takes the earth takes slightly over 365 days to revolve around the sun. The fact that it is approximately 365.25 days should mean that leap year should come every fourth year.
But, things are a bit more complicated than that because one revolution around the sun is almost but not quite 365.25 years, so leap years come slightly less often than once every four years. To figure out if a year (say, 1999) is a leap year, you need to test whether it is divisible evenly — that is, if there is no remainder after the division — by three different values.
A calendar year is a leap year if
- it can be divided evenly by 4,
- unless it can also be divided evenly by 100, in which case it is not a leap year,
- except if it is also divisible by 400, in which case it is a leap year.
(We aren't making this up.)
So, the year 2000 was a leap year (divisible evenly by 400, 100, and 4),1900 was not (divisible evenly by 100 and 4 but not by 400), 2012 was (divisible evenly by 4 but neither 100 nor 400), and 2015 wasn't (not divisible by 4).
-
Consider the block sets below: they all say "leap year" if the
year variable is a leap year and "normal year" otherwise. That is, they all work correctly, without any bugs. (The scripts are available in this snap program).
-
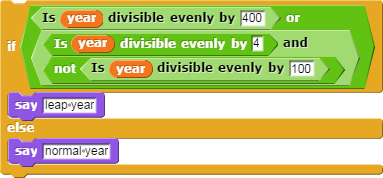
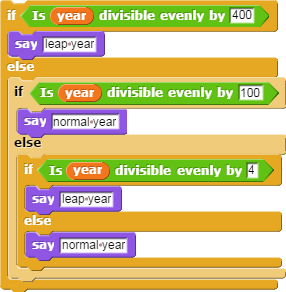
Discuss with others which version you prefer, and defend your answer.
- Which one is easiest to read?
- Which one would be easiest to rewrite from memory?
- In which one would it be the easiest to find a bug?
- Which one is the most beautiful?!