Sequential Languages

A programming language is characterized by two things: a philosophy of programming and details of notation. Most modern programming languages are multi-paradigm but basically sequential. This includes Snap!, even though you have learned some composition (nesting) of functions (known as functional programming) and some ideas about sprites as objects (object-oriented programming).

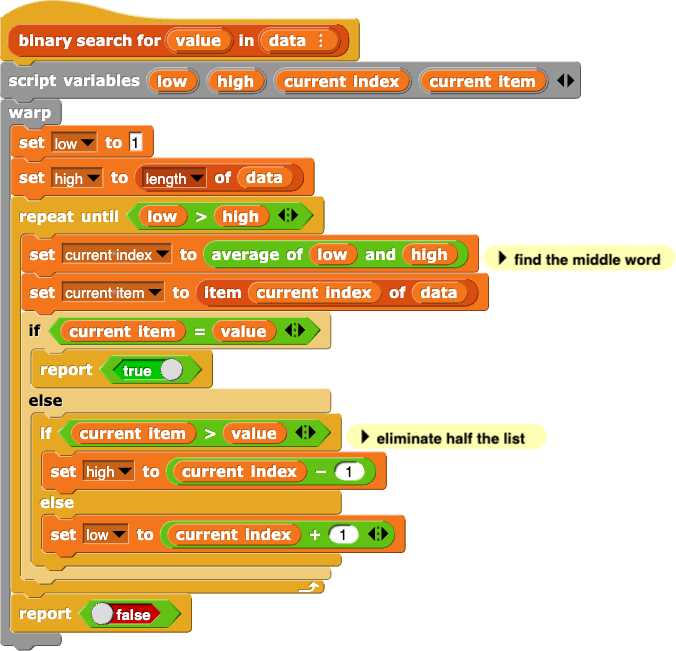
Learning another language of the same type is much easier than learning your first one. For example, here’s the binary search function from Lab 1 of this unit:

Python

Here's the same procedure written in Python:

def binary_search(value, data):
    low = 0
    high = len(data)-1
    while (low <= high):
        current_index = average(low, high)    # find the middle word
        current_item = data[current_index]
        if (current_item == value):
            return True
        elif (current_item > value):          # eliminate half the list
            high = current_index-1
        else:
            low = current_index+1
    return False

For the most part, this is line-for-line the same as the Snap! version, apart from tiny details such as

return

instead of . There are also several more significant differences in notation.

JavaScript

Here's the same binary search procedure written in JavaScript:

function binarySearch(value, data) {
    var low, high, currentIndex, currentItem;
    low = 0;
    high = len(data)-1;
    while (low <= high) {
        currentIndex = average(low, high);    // find the middle word
        currentItem = data[currentIndex];
        if (currentItem == value) {
            return true;
        } else if (currentItem > value) {     // eliminate half the list
            high = currentIndex-1;
        } else {
            low = currentIndex+1;
        }
    }
    return false;
}

This doesn't look so different from the Python version, but there are a few significant differences.

There are things to learn about notation (syntax, which is the text-language equivalent of block colors and shapes). But you would be able to learn the details of one of these other languages much more quickly than you learned Snap! because you already know how to program in a sequential langauge.

Snap! Primitives in Other Sequential Languages

Central programming language features having to do with flow of control (), data management ( and ), and computation ( and a few blocks) have direct equivalents in most languages. Here are a few examples:

Snap!	Python	JavaScript
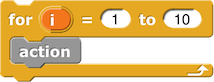	for i in range (1, 11): action()	for (i=1; i <= 10; i++) { action() }
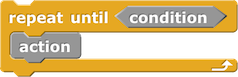	while (not condition): action()	while (not condition) { action() }
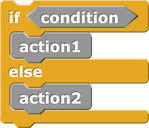	if condition: action1() else: action2()	if (condition) { action1() } else { action2() }
	yes if condition else no	(condition ? yes : no)
	return value	return value
	return	return
	lambda x : some_function(x)	function (x) { return someFunction(x) }   or (x) => someFunction(x)
	a * b	a * b
	a ** b	a ** b
	a and b	a && b
	" ".join(["hello","world"])   or "hello " + "world"	"hello".concat(" ","world")   or "hello " + "world"
	foo = 87	foo = 87
	foo += 5	foo += 5
	["John", "Paul", "George", "Ringo"]	["John", "Paul", "George", "Ringo"]
	value[0]	value[0]
	value[1:]	value.slice(1)
	list(map(some_function, value))   or [some_function(x) for x in value]	value.map(someFunction)
	for item in value: action(item)	value.forEach(action)

This is just a small sample of the number of primitive commands and functions in any programming language. Luckily, you don't have to memorize them; you can do a web search for "javascript list item," for example, to learn any particular one as you need it.

By the way, look at the Python join in the table. It has the very nice feature of allowing you to choose a separator to go between the joined strings:

>>> " ".join(["John", "Paul", "George", "Ringo"])
'John Paul George Ringo'
>>> ",".join(["John", "Paul", "George", "Ringo"])
'John,Paul,George,Ringo'

In the first interaction, the string " " provides the separator; in the second, the string "," does. That's an elegant way to extend the idea of joining strings, avoiding the need to put spaces in the input strings. (You could also use an empty string to get the exact effect of the join block in Snap!.)

But look at the Python equivalent of for. Why does range(1,11) mean "the numbers from 1 to 10"? The idea is that you're using those numbers to select items from a list, but instead of numbering the items, Python numbers the spaces between items, just as when you're using a word processor it displays the cursor as a vertical line between two letters. So range(1,11) means "the items to the right of gap number 1 and to the left of gap number 11." You can learn to think that way, but it's not obvious to a beginner. (It's a little more intuitive if you start at position 0, before the beginning of the list; range(0,5) selects five items from a list, and you can abbreviate it as range(5).)

What do you think about using + to join strings? It's meant as an analogy with arithmetic; you are "adding" one string to another. Using the same symbol to mean two different things in different contexts is called "overloading." It's not too bad in Python, which is very strict about the distinction between a number and a string of digits. (2+"3" gives an error message.) But JavaScript, like Snap!, will automatically convert a number into a string of digits if necessary, so 2+"3" is "23" even though 2+3 is 5. (The automatic conversion isn't a problem in Snap! because Snap! doesn't overload the + operator.)

The other block categories, the ones having to do with graphics or sound, don't really have analogs in other languages. Instead, just as Snap! has libraries, other languages also have libraries to provide such capabilities. For example, if you want JavaScript equivalents to the turtle graphics blocks (move (n) steps, etc.), you start in your search engine; "JavaScript turtle graphics" will get you to https://github.com/bjpop/js-turtle from which you can download the file "turtle.js" to include with your own JavaScript program. (On the other hand, because the main purpose of JavaScript is writing programs that will be run inside a browser window, it does have built-in support for the sort of graphics you see in typical browser windows: scrolling text boxes, form-filling, checkboxes, etc.)

Libraries are a little easier in Python because there's a central repository of them. So you can draw a square this way:

from turtle import *

pendown()
for i in range (4):
    forward(100)
    right(90)

Non-Sequential Languages

In the early days, all programming languages were sequential, because that's how computer hardware works, and higher level languages were seen as a convenient abbreviation for machine language, rather than as a source of abstraction. Since then, several types of programming language based abstraction ("programming paradigms") have been invented. Most modern languages have some aspects of most of these, but in this section you'll learn about languages that are entirely based on one particular paradigm. It's worthwhile to learn such a language because it will immerse you in how things are done in that paradigm, even if in real life you end up programming in a mixed-paradigm language such as Snap!, Python, or JavaScript.

Functional Programming in Haskell

Imagine if Snap! had only reporters and predicates, with no command blocks. To perform a computation, you'd build up an expression in the scripting area, then click on it to see the result in a speech balloon. You could make script variables, but you'd give them a value at the time you create them, and you couldn't then change the value. That would be a functional programming language.

Here's the same binary search algorithm shown above, written in Haskell, a purely functional language:

find :: Ord a => Array Int a -> a -> Maybe Int
find arr x = uncurry (search arr x) (bounds arr)

search :: Ord a => Array Int a -> a -> Int -> Int -> Maybe Int
search arr x lo hi
  | hi - lo + 1 == 0 = Nothing
  | x == el = Just mid
  | x > el = search arr x (mid+1) hi    -- eliminate half the list
  | otherwise = search arr x lo (mid-1)
  where mid = (hi + lo) `div` 2         -- find the middle word
        el = arr ! mid

Source: exercism.io, CC-BY-SA

This looks very different from the other programs you've seen, but don't throw up your hands in despair. You're not expected to be able to learn to program in Haskell in just a few days, but you can read this example with some help. Start with the fourth line, search arr x lo hi; it's like the hat block that begins a Snap! procedure, in this case a search procedure with four inputs.

In search you'll see functional programming making a difference in the programming style. The Snap! version of the program is organized as a repeat until loop, in which the values of the variables low, high, current index, and current item are changed on every repetition. If you're not allowed to change variables' values, what can you do instead?

The answer is that search calls itself recursively, in the lines

  | x > el = search arr x (mid+1) hi
  | otherwise = search arr x lo (mid-1)

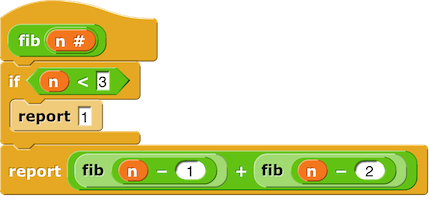
If you try to trace through computing fib 4 on the assumption that there's a single variable n shared by all the recursive calls, you'll get the wrong answer.

The where in the last two lines of the program is how Haskell creates script variables and gives them their (unchanging) values.

The four lines that start with vertical bars (|) are like a set of nested if/else blocks: If hi is one less than lo, return nothing. If the value you're looking for is equal to item mid of arr, return the index mid. (This version of binary search returns the position of the value in the list, if any, instead of just True.) If the value you want is more than the value at the midpoint, search from the midpoint to the end of the list. Otherwise, search from the beginning of the list to the midpoint.

Could you tell me more about functional programming?

The two lines with Ord a and so on are type declarations. Such declarations aren't a necessary part of a functional language, but the main functional languages do use them. The "a" on those lines is the name of a data type that's being created in each declaration. Find and search are of type "function," but not any old function. Find is of type "function that takes as inputs an array (like a Snap! list) of values of type a, which has to be an Ordered type (because binary search doesn't make sense otherwise), and a single value of type a, and returns either an integer or nothing at all." Looking at this another way, each of those lines creates an abstract data type. (The name a is local to each function.)

 

Find is the main procedure; search is a helper function. Note that find takes two inputs, arr for the array and x for the value to be found. Search, though, takes four inputs: arr, x, lo for the lowest array index to examine, and hi for the highest index. So how can find say (search arr x), calling search with only two inputs?

This is part of what it means to take function-as-data seriously. When you call any Haskell function with fewer inputs than it expects, it returns a function of the remaining inputs, sort of as if when you defined

you automatically also got this one:

and similarly for one-input and three-input versions. Turning a function into a function with fewer inputs is called currying it, named after Haskell Curry, a mathematician who contributed to the early development of lambda calculus, the mathematical basis for functional programming. So the call to uncurry turns the two-input function back into a four-input function by supplying the missing two inputs, namely (bounds arr), a function call that reports the lowest and highest indices of the array, which will be 0 and the array length minus 1.

Even if you're convinced that functional programming is a good idea (which it is, because it avoids the kind of bug in which two parts of the program are using the same variable for different purposes, and because functional code turns out to be the easiest to parallelize for multi-processor machines), why would you choose a language that forces you to program in that style? Well, many people don't. You can, if you're disciplined about it, program functionally in any language that's functional enough to include higher order functions, which are an important benefit of functional programming. (You did something like this in the Tic-Tac-Toe project, not in the part that displays moves on the stage, but in the part that computes the best move for the computer. That computation is one function calling another: calls , which calls , which calls , which calls .) But a purely functional language helps eliminate program bugs, which is especially important when a team of programmers work together on the same program. And compilers for functional languages can take advantage of the constraints of functional programming to generate very efficient programs. In any case, learning a purely functional language ensures that you discover every aspect of functional programming.

Object Oriented Programming (OOP) in Smalltalk

Imagine if in Snap! you could make only sprite-local procedures and variables, not global ones. Imagine also that everything in the language were like sprites in that way. So, for example, imagine that the number 3 had its own procedures—its own + and so on. Something that has its own local procedures (called methods) and its own local variables (often called fields, depending on the language) is called an object.

It would be unusable if you actually had to write a + method for 3 and a different one for 4. But think about making clones of a sprite, as you did in the Tic-Tac-Toe project. Each clone inherits the methods and some other attributes from its parent sprite. Similarly, 3 and 4 are instances of the class (type of object) Integer, which in turn inherits from the class Number. You can think of an object class as a souped-up abstract data type with methods other than just its selectors.

So, what happens when you say 3 + 4? You are sending the message + 4 to the object 3. (In Snap!, the broadcast block sends a message to all objects, and the tell and ask blocks send a message to a specific object.) The message + 4 consists of a keyword, +, along with an input, 4.

These days, most programming languages are sort of object oriented, just as most sort of support functional programming. For example, in the translation table above, the translation of the map block to JavaScript is value.map(someFunction). Map takes two inputs, a function and a list. Python expresses that idea as a two-input function, map(some_function,value). Why does JavaScript put one of the inputs in front of the function name? The reason is that JavaScript's map isn't a global procedure; it's the keyword of a message that you can send to a list. Their message-passing syntax is object.keyword(inputs).

But most languages don't go so far as to treat numbers as objects. In most languages, including Snap!, + is a global function that takes two numbers as inputs. The only widely known language that's truly object oriented, in which everything is an object, is Smalltalk, the language that introduced object oriented programming to the world.

Here's the binary search program in Smalltalk:

SequenceableCollection >> binaryFindIndexOf: aNumber left: leftIndex right: rightIndex
      | middle |
      leftIndex = rightIndex ifTrue: [ ^ 0 ].
      middle := (rightIndex + leftIndex) // 2.  "find the middle word"
      ^ (self at: middle) = aNumber
            ifTrue: [ middle ]
            ifFalse: [
                (self at: middle) > aNumber     "eliminate half the list"
                    ifTrue: [ self binaryFindIndex: aNumber left: leftIndex right: middle - 1 ]
                    ifFalse: [ self binaryFindIndex: aNumber left: middle + 1 right: rightIndex ]
            ]

Source: stackoverflow.com, CC BY-SA, and Bernat Romagosa

The first line of this program says that it is adding a new method to the class SequenceableCollection, which is a parent class of arrays, lists, and other kinds of sequences of items. The corresponding message has three keywords, binaryFindIndexOf:, left:, and right:. This is similar to the way Snap! blocks can have title text mixed with input slots. The inputs to this method are named aNumber (a Smalltalk convention that helps make the code self-documenting because we know what kind of object it expects), leftIndex, and rightIndex. (Shouldn't there be an input for the collection in which the method will search? No, because that collection is an object, and binaryFindIndexOf is a method of the collection.)

The vertical bars in the second line are the Smalltalk syntax for script variables. Another noteworthy piece of syntax is that Smalltalk uses square brackets [ ] the way Snap! uses gray rings, surrounding a piece of code that can be input to a message. Smalltalk sensibly uses = to mean the equality test; its equivalent to set is the two-character sequence :=. (Smalltalk was developed long before Unicode; if they were designing it today they'd probably use ←. The hat (^) is like report. The double slash // is division with the result rounded to an integer.

The Boolean values True and False are, of course, objects; they accept messages with keywords ifTrue: and ifFalse:, each of which takes a code block (in square brackets, in this program) as input. So there's no need for an explicit if procedure.

The name self refers to the object that is carrying out the method, like or in Snap!. The message at: middle, sent to a collection, means the same as item middle of collection in Snap!. The rest of the program should now make sense.

Could you tell me more about object oriented programming?

Object oriented programming with message passing does a great job with functions of one input, such as asking a list for its length. It's a little more awkward for a function like +, whose two inputs really play mathematically similar roles. Saying that 3 is the actor and 4 is just an input feels peculiar. Some languages try to overcome this issue by using generic functions instead of message passing. That means that you could define functions sum(integer,integer), sum(integer,float), and so on, so that all the inputs help determine which method is used. When you call a function, the language looks for the best fit between the methods you've defined and the classes (types) of the inputs.

Think about Python's " ".join(["hello","world"]) notation. This is the same object.method(inputs) syntax that JavaScript uses, and it works well. But it seems a little strange that what you're supposed to think of as the active object is the delimiter character, rather than the meaningful strings you're combining. Compare that with JavaScript's "hello".concat(" ","world"), which makes the first string the actor and other strings, including delimiters, the inputs. That seems more Smalltalk-like.

 

Smalltalk is a class/instance language. That means that there's a special kind of object called a class that contains all the methods for any object of that class. For example, Integer is a class, and 3 is an instance. The inheritance of methods from parents happens in the classes, not the instances.

As you know, Snap! takes a different approach. Every object combines the features of classes and instances; it can have methods and can inherit, like a class, but it's a specific value, like an instance. (For example, sprites can have methods, and can inherit them, but a sprite can be shown on the stage and move around, like an instance.) This approach is called prototyping OOP.

Many languages that purport to use prototyping (JavaScript, for example) have a special kind of object called a "prototype," and that's the kind of object that can have methods and a parent. If you're asking yourself "How does that differ from a class?" you're right. Snap!'s prototyping is both simpler and more flexible.

Why would you use an object oriented language? Programmers' opinions on this question have changed dramatically over time. When Alan Kay and his team at Xerox PARC introduced Smalltalk, very few people got the point. But today, there are many programmers who insist that using anything other than object oriented programming is professional malpractice. (They don't use Smalltalk, though; many use Java, the language of the College Board AP Computer Science A course.) The main thing that's made OOP so popular is information hiding, which means that one object can't directly examine another object's variables or call its methods, but must instead send the target object a message that it accepts from other kinds of objects ("public messages").

Ironically, information hiding isn't a necessary part of OOP. In Smalltalk, any message an object understands can be sent to it by other objects. (There are no private methods.) In a language for learning, such as Smalltalk in its early days and Snap!, information hiding isn't important. Programs are small, and they have just one or two authors. (The people who talk about malpractice are thinking about teams of 500 programmers, and all the ways they can step on each others' feet unless the objects each one programs are protected from each other.) That's why Snap!, like Smalltalk, allows an object to call any method of another object, not just a few for which the other object publishes messages. Snap!'s developers were more interested in one of Smalltalk's central ideas: simulation.

In pre-OOP programming, there's one program running all the time, and it's in charge of all the necessary computations. That's fine if you're computing a function, for example, but some programs are meant to model the behavior of a complex system with many independent actors, such as the disease simulation project in this unit. The simple model used in that project has only one object type, people. A better model would have different kinds of people (for example, those who do and those who don't follow medical advice about wearing masks) and would model the disease itself, such as its ability to mutate. OOP is great at this kind of simulation, because each object is responsible for its own behavior. (Scratch, from which Snap! inherited the idea of sprites, was originally implemented in Smalltalk, whose influence is seen in such details as multi-keyword block names, as well as in the organization of a program as scripts that belong to specific sprites, with no central program.)

Declarative Programming in Prolog

This section isn't going to start with "Imagine if Snap!..." Declarative programming is a very, very different approach. What you have to imagine is that programs don't have algorithms!

Instead, a program consists of facts and rules that you are teaching the computer. One of the standard examples is about family trees. "Brian's mother is Tessa" is a fact, a specific piece of information.

mother('Brian','Tessa').

grandmother(A,C) :-
    mother(A,B),
    mother(B,C).

What about the mother of someone's father? Shouldn't that have to be in the rule, too? The answer is that you can have as many rules as you want about grandmotherhood:

grandmother(A,C) :-
    father(A,B),
    mother(B,C).

Once you've taught the computer some rules and facts, you can ask questions, such as "Who is Brian's grandmother?":

?- grandmother('Brian', X)

A very important difference between declarative programming (also called logic programming) and the other paradigms you've seen is that a question may have more than one answer! This is very different from a function, which can only report one value. Prolog doesn't just pick one answer to show you; it shows all the answers it can figure out from the information it has (one at a time). Here's an example:

?- append(X,Y,[a,b,c,d]).
X = [],
Y = [a, b, c, d] ;
X = [a],
Y = [b, c, d] ;
X = [a, b],
Y = [c, d] ;
X = [a, b, c],
Y = [d] ;
X = [a, b, c, d],
Y = [] ;
false.

The user has asked "what two lists can be appended together to get the list [a,b,c,d]?" There are five possible pairs of lists that satisfy the condition. Prolog prints the first answer (shown in yellow above), then waits for the user to type the space key or semicolon, then displays the next answer, and so on. When the user asks for a sixth answer, the result is "false," which means that Prolog can't find any more values for X and Y that make the query true. (That doesn't mean it's proven false; for example, if you teach Prolog about your family tree and then ask questions about someone else's family, Prolog won't find any information, but that doesn't mean the other person really doesn't have any relatives.)

Wow! Snap! has an function; you can ask it questions such as "what do I get if I append the list [a,b] and the list [c,d]?" But you can't "run it backward," asking questions such as "What must I append to [a,b] in order to get [a,b,c,d]?" let alone "What two lists can I append to get [a,b,c,d]?" But Prolog's append isn't a function of two lists; it's a relation (you can think of it a predicate function, although you shouldn't forget that it's not really a function, running an algorithm, at all) among three lists, which is True if the result of appending the first two inputs is the third input. There's no special magic in append; if it weren't predefined in Prolog, you could define it this way:

append([],Z,Z).

append([A|X],Y,[A|Z]) :- append(X,Y,Z).

The notation [A|B] represents a nonempty list whose first item is A and whose all-but-first is B. The first rule says that if you append an empty list and any list Z, you get Z. The second rule says that if the first list isn't empty, then the first item of the result must be the first item of the first list, and the rest of the result must be the result of appending the rest of the first list and the second list.

Okay, time for binary search in Prolog:

contains(List, Value) :- even_division(_, [Value|_], List).

contains(List, Value) :-                          % eliminate first half of list
    even_division(_, [Center|SecondHalf], List),
    Center < Value, SecondHalf \= [],
    contains(SecondHalf, Value).

contains(List, Value) :-                          % eliminate second half of list
    even_division(FirstHalf, [Center|_], List),
    Center > Value, FirstHalf \= [],
    contains(FirstHalf, Value).

even_division(First, Second, Xs) :-               % find the middle word
    append(First, Second, Xs),
    length(First,F),
    length(Second,S),
    S >= F, S-F =< 1.

Source: colby.edu

The first thing to say about this program is that it's not really a good model of how to program in Prolog. The helper rule even_division wants to divide a list into two equal-size pieces; it ends up dividing the list into two pieces every possible way (like the append example earlier), and then checks each of those divisions to find one whose two pieces are the same length. If you really wanted to do a binary search in Prolog, you'd do it by using a more complicated data structure that comes pre-divided into equal size pieces. But for the purpose of this lab, comparing languages, it's best to use the same structure in all the sample programs.

The underscore character _, used by itself, means that you don't care what value goes in that slot in the program. (Underscores can also be used as part of a variable name or a relation name, as in the relation even_division.)

So the first rule

contains(List, Value) :- even_division(_, [Value|_], List).

means that the given Value is in the List if it happens to be the middle item of the list—that is, List can be divided into two equal parts, you don't care what's in the first part, and the second part has Value as its first item, followed by some values you don't care about.

The next rule handles the case in which the value is larger than the middle item of the list. It says that List contains Value provided that the middle item Center is less than Value, the second half of List has items other than just Center, and those other items (SecondHalf) include the desired Value. (The requirement that SecondHalf isn't an empty list is there to prevent infinite loops in which the program keeps dividing an empty list into two (equal size) empty lists.)

Similarly, the third rule handles the case in which the value is smaller than Center.

Why isn't there a rule saying to report False if the value isn't found? This is the mind-stretching part of declarative programming. A rule isn't a function, and it doesn't report a value. That would be an algorithm! A rule doesn't do anything; it's just another kind of data. If Prolog can't match the question you ask against any combination of facts and rules, then you just don't get an answer at all. That's not considered an error.

The use of even_division in this program is an attempt to have it work the way binary search works, by dividing the list in half at each step. But if you just want to know if a value is in a list and aren't worried about efficiency, the entire program could be replaced by one rule:

contains(List, Value) :- append(_, [Value|_], List).

This says that the list can be divided into two pieces (the first of which might be empty; you don't care what's in it), such that the desired value is the first item in the second piece of the list. That example should give you some feeling for the power of the declarative programming notation.

How does a Prolog program actually work? If there are no algorithms, only data, how can any matching of queries to things in its database happen? The answer is that the language itself implements a single, universal algorithm, called resolution, that will always find every answer to a question you ask that can be deduced from the database, provided that it doesn't get caught in an infinite loop. (If resolution could guarantee the impossibility of infinite loops, it would solve the Halting Problem, which you know can't be done.)

Could you tell me more about declarative programming?

The Prolog database consists of facts and rules. The difference is that facts don't contain variables. So, given a query such as mother('Brian',X), it's pretty easy to see whether that matches a fact such as

father('Brian','Len')	Nope, father≠mother
mother('Bob','Tessa')	Nope, 'Bob'≠'Brian'
mother('Brian','Tessa')	Yes, provided that X='Tessa'

The only subtlety is that if the same variable is used twice in a query, it has to match the same text every time, so that someone who says mother(X,X), presumably wanting to find someone who's their own mother, doesn't match every fact about mothers in the database.

Rules are more complicated, because both the query and the rule can have variables. Consider the query append(X,Y,[a,b,c,d]) that you saw earlier. If the same variable name is used twice in the same query, or in the same rule, that name must match the same value each time it's used. But it's okay for a user to use a variable name in a query that happens to be the same as a name used in a rule; they don't have to have the same value. It's like using the same name in a script variables block in two different scripts; they're different variables despite the coincidence of the names.

So, when trying to match a query against a rule, the first step is to systematically rename all the variables in the rule, with unique names. For example, the first time Prolog compares a query with the rule

append([],Z,Z).

it (temporarily) changes the rule to something like

append([],Z.1,Z.1).

The next time it compares something to that rule, it'll change it to

append([],Z.2,Z.2).

And so on.

Okay, compare the append query above with this first rule:

append(X,Y,[a,b,c,d]).
append([],Z.1,Z.1).

This results in the following pairings:

X = []
Y = Z.1
Z.1 = [a,b,c,d]

Combining the information in the last two of those pairings gives Y = [a,b,c,d], so that gives both of the variables in the query values, so Prolog gives the first answer.

That was a simple rule, in that its conclusion always holds. The other append rule includes a condition that must be true in order for the rule to apply. After renaming, that rule says

append([A.2|X.2],Y.2,[A.2|Z.2]) :- append(X.2,Y.2,Z.2).

The resolution rule for rules with conditions is that first we try to match the query with the conclusion of the rule, then if that works, we take the condition of the rule as a new query. In this case, we are comparing

append(X,Y,[a,b,c,d]).
append([A.2|X.2],Y.2,[A.2|Z.2]).

The technical name for matching two expressions that can both contain variables is unification. Figuring out exactly how to get it right is hard, but luckily, it's been done, so you don't have to. Here are the results:

X = [A.2|X.2]
Y = Y.2
[A.2|Z.2] = [a,b,c,d]

But now think about what the [...|...] notation means. That last match can be expressed as the two matches

A.2 = a
Z.2 = [b,c,d]

This isn't enough to give us values for X and Y in the original query with no variables in the values. But knowing that A.2 must have the value a is a big step forward. It tells us that X is a list whose first item is a.

Now, remembering all the pairings so far, we start again with the query append(X.2,Y.2,Z.2). Compare that with the first append rule:

append(X.2,Y.2,Z.2).
append([],Z.3,Z.3).

From this we learn

X.2 = []
Y.2 = Z.3
Z.2 = Z.3

This might be dizzy-making for people, but luckily computers don't get dizzy. Here again are all the matches Prolog has found for this second answer:

X = [A.2|X.2]
Y = Y.2
[A.2|Z.2] = [a,b,c,d]
A.2 = a
Z.2 = [b,c,d]
X.2 = []
Y.2 = Z.3
Z.2 = Z.3

You can trace through these equations to learn that

X = [A.2|X.2] = [a|[]] = [a]
Y = Y.2 = Z.3 = Z.2 = [b,c,d]

and that's the second answer. We'll stop here, but if you want you can match the query

append(X.2,Y.2,Z.2)

against the second rule, and the result of that against the first rule, and so on.

Why would you program in a declarative language? Some problems just lend themselves to a database-ish frame of mind. Think about family trees again. There may be gaps in what you know about your ancestors; an algorithm that expects everyone in the database to have exactly two parents in the database wouldn't work if there's missing information. Similarly, if you have two mothers or two fathers, a situation that's more common these days than in the past, Prolog won't mind. You just tell it two facts such as mother('me','mom1') and mother('me','mom2'). Also, nothing beats declarative programming for situations in which a problem can have more than one answer. Think about a quadratic equation with two solutions. In ordinary programming, you can write a function that reports a list of two numbers, but a list isn't a number, and can't take part in further numeric computations. It's better if you get two separate answers, each of which is a number.

The Morals of the Story

So, one overall moral of this story is that if you have the urge to learn more programming languages, you'll be intellectually better off learning Haskell, Smalltalk, or Prolog, rather than learning a bunch of languages that are pretty much all the same, such as JavaScript, Python, C, Java, and so on. (If you want a programming job this summer, though, you might need to learn the language a potential employer wants to use.)

And, by the way, don't think that because this page is telling you about other languages it means you've learned all there is to know about Snap!. For example, read Sections VIII (OOP with Procedures) and X (Continuations) in the Snap! Reference Manual.

But also, bear in mind that learning computer science doesn't mean learning a lot of programming languages. If you study CS at the university level, you won't be taking classes named after programming languages; they'll have names like "Algorithms and Data Structures," "Graphics," "Operating Systems," "User Interface Design," "Compilers," "Recursive Function Theory," and so on. Maybe instead of learning another language, you should work your way through Structure and Interpretation of Computer Programs, the course that separates the wizards from the muggles.