-
"Flat line ends" should be unchecked for this one.
Here is a block and the picture it makes.

(color-0).png)
Edit it and give it inputs that let you produce pictures like these. You don't have to use script variables.
(color-0).png)
(color-0).png)
(color-50).png)
(color-50).png)
Experiment with various inputs.
-
The artist Joseph Albers became famous for paintings a bit like this:
(color-60).png)
(color-60).png)
Set "flat line ends" and create a block that draws pictures like this. It will be convenient to use script variables
- Edit your
raise (n) to the power (b) block to make it work for negative integer exponents.
-
Old-fashioned divisibility test—divisibility by 3 or 9:
- Create a helper reporter
digit sum that adds up the digits in a number. So, for example digit sum 7 should report 7, and digit sum 12 should report 3, and digit sum 126 should report 9 (the sum of 1, 2 and 6). You may find these blocks useful. 

- Then write
repeated digit sum, which keeps taking the digit sum until the result is a single digit. For example, the digit sum of 238 is 2+3+8=13, which is more than a single digit. The digit sum of 13 is 1+3=4, which is a single digit. So the repeated digit sum of 238 is 4.
-
Write predicates
divisible by 3? and divisible by 9?. A number is divisible by 3 if its repeated digit sum is 0, 3, 6, or 9; it's divisible by 9 if its digit sum is 0 or 9.

 Why?
Why?
-
Old-fashioned divisibility test—divisibility by 7:
Create a
multiples of 7 algorithm block that takes any whole number as input and then puts it through this process:
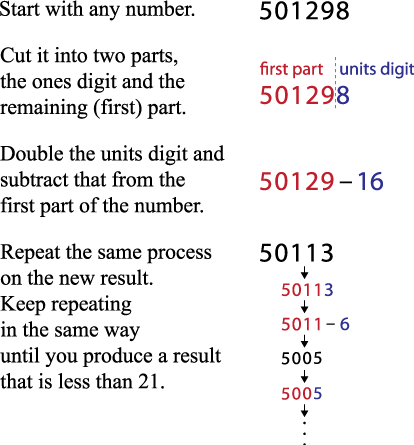
Test it first on several multiples of 7 (small and large) and make sure that, for multiples of 7, it reports only the results 14, 7, 0, -7, and -14. Also test it on several numbers that are not multiples of 7; for those numbers, it should never report 14, 7, 0, -7, or -14. .png)
- Look up a test for divisibility by 11 or 13 and see if you can build a block that performs that algorithm.
In snap, as in most programming languages, you can test for divisibility just by using mod, but before computers were widespread, algorithms like these greatly simplified some computations.

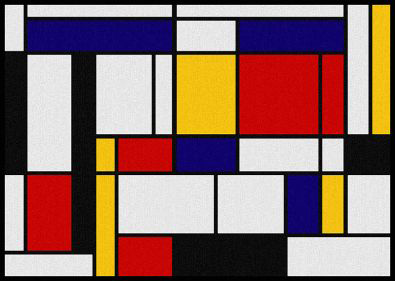 "Tableau 1" by Piet Mondrian
"Tableau 1" by Piet Mondrian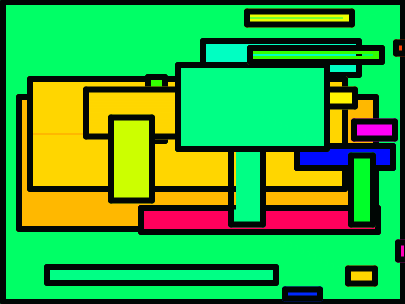


.png)
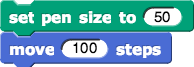 does not do what you might expect, because the "ends of the lines" are rounded. Try it. Now
does not do what you might expect, because the "ends of the lines" are rounded. Try it. Now  .
.

 and
and as-letter.png) will help you do that. Experiment with them to see how they work.
will help you do that. Experiment with them to see how they work.-withresult(iboez).png) .
.
 (or
(or  ) that takes a positive integer n and reports the product of all whole numbers from 1 through n, in other words 1 × 2 × 3 × ... × (n - 1) × n. When the input is 4, the output should be 24 (because 1 × 2 × 3 × 4 = 24).
) that takes a positive integer n and reports the product of all whole numbers from 1 through n, in other words 1 × 2 × 3 × ... × (n - 1) × n. When the input is 4, the output should be 24 (because 1 × 2 × 3 × 4 = 24).
.png) because 5 factorial is really just 5 times 4 factorial. Using your block, check each of these computations—
because 5 factorial is really just 5 times 4 factorial. Using your block, check each of these computations— ,
,  ,
,  and
and  —to see what it reports. One of these is inconsistent with the others. To fix the problem, we need to define 0! = 1. Edit your
—to see what it reports. One of these is inconsistent with the others. To fix the problem, we need to define 0! = 1. Edit your  should not work. Check to see what does happen. Then edit your block and find a way to use
should not work. Check to see what does happen. Then edit your block and find a way to use  to check that the input is a number and report some sensible result or message.
to check that the input is a number and report some sensible result or message. reports a result.
Find out what it reports and analyze what the block does so that you can figure out why that is the result.
reports a result.
Find out what it reports and analyze what the block does so that you can figure out why that is the result.
 so that
so that  reports the sum 3 + 4 + 5 + 6 + 7, and
reports the sum 3 + 4 + 5 + 6 + 7, and  reports the sum of -3 + -2 + -1 + 0 + 1 + 2 + 3.
reports the sum of -3 + -2 + -1 + 0 + 1 + 2 + 3..png) because, from 1 through 8, only the numbers 1, 2, 4, and 8 evenly divide 8.
because, from 1 through 8, only the numbers 1, 2, 4, and 8 evenly divide 8. 
(color-0).png)
(color-0).png)
(color-0).png)
(color-50).png)
(color-50).png)
(color-60).png)
(color-60).png)


 and
and  are useful. They are in
are useful. They are in 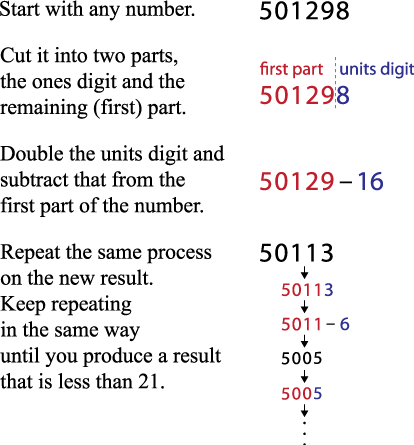
.png)
 style of programming is very common, pretty soon you'll learn a better way: functional programming, in which you never change the value of a variable. You're not quite ready to write functional programs yet (that'll come in Unit 3), but here are some examples from above, rewritten functionally, that you can probably understand:
style of programming is very common, pretty soon you'll learn a better way: functional programming, in which you never change the value of a variable. You're not quite ready to write functional programs yet (that'll come in Unit 3), but here are some examples from above, rewritten functionally, that you can probably understand:

