-
Art idea: The code
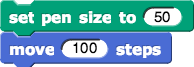 does not do what you might expect, because the "ends of the lines" are rounded. Try it.
does not do what you might expect, because the "ends of the lines" are rounded. Try it.
Now clear the stage and try  .
.
Why does that happen?

Experiment with the possibilities...


You can choose between flat and round ends in the settings menu.
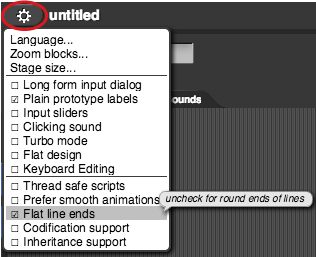
If you switch to "Flat line ends" for this project, you will probably want to switch back to "round ends" for other drawing projects.
Artists use tools: brushes, cameras, pencils, computers. Asking a computer to paint some random picture may not be art, but when you have designed the algorithm, tested it, changed it until you like how it works, and selected your favorite examples, you are being the artist. The computer is then just the tool.
-
Mondrian art project: The Dutch artist Piet Mondrian is possibly best known for his artwork using brightly colored rectangles.
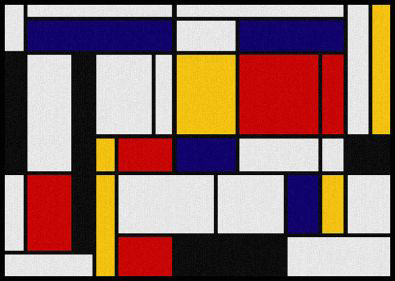 "Tableau 1" by Piet Mondrian
"Tableau 1" by Piet Mondrian
Mondrian wasn't at all random in his choice of colors and locations, but even some random choices can be interesting. A snap script can produce designs like these.
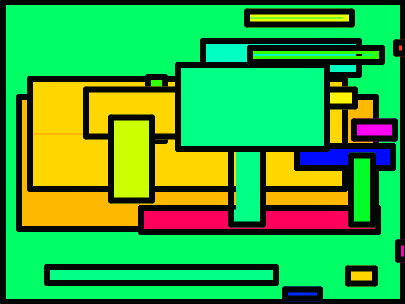

This isn't the actual Snap! program. You could write custom blocks with these names, but they're a little verbose to use as real block names, especially that two-line one in the middle. This algorithm is for you to read, not for a computer to read.
This algorithm produced those designs:
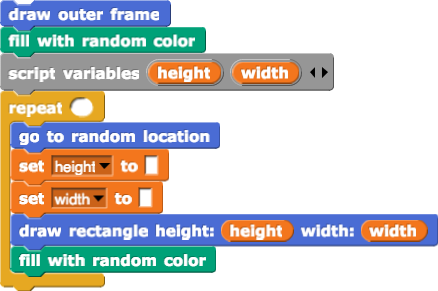
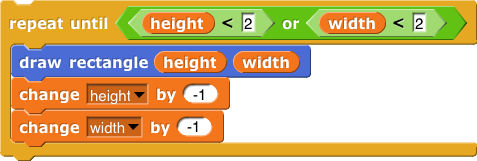
To keep your code clear, you may want to create separate blocks that specialize in boundary and fill and choosing locations and calculating size.
If you've been working with the version of this project that uses Snap
!'s
fill block, you can find that version
here. Although, some people have found the way that block works to be frustrating for this project.
One way to make a
fill with random color block is:
Another way is to draw a single line with a very wide width (using "flat line ends" from the Snap
! Settings menu) and then drawing a rectangle around it.
To get bright colors, use
set pen shade to 100. You can get a good collection of colors with:
.png)
- Take screen shots of the artworks your program generates and save the ones that you like best.
- Mondrian limited his colors and used a lot of white and some black. Experiment with that to see if you get designs you like.
- Find ways to improve your program.
-
Writing secret code: You will create an encoder/decoder with
for, length of, letter of, join, the unicode blocks.
- In order to do this, you will need to be able to change a letter into a number, add 1 to that number, and then change the new number back to a letter. The Snap! blocks
 and
and as-letter.png) will help you do that. Experiment with them to see how they work.
will help you do that. Experiment with them to see how they work.
- Create a block
encode that takes a word as input, changes each letter into the next letter in the alphabet—for example, A becomes B, Y becomes Z...—and reports the result, like this: -withresult(iboez).png) .
.
Unicode is a computing standard that includes characters from all human languages—including mathematics, Elvish, and Klingon.
encode adds 1 to the unicode for each letter. You could, instead, add 2 or 5 or.... Give encode a second variable that lets you specify what to add to the unicode.- When you give
encode the input z, what does it report? If that's not what you would like it to report, change it.
- Make a
decode block.
- Linguistic research: Build a block that takes text as input and says which letter, t or s, is used more often in that text. Later, you'll be able to generalize to take a chunk of text and figure out the frequency of each letter. Letter frequency differs from language to language. That information has been used as one clue in decoding encrypted messages.
-
A mathematical function: Create a
factorial block  (or
(or  ) that takes a positive integer n and reports the product of all whole numbers from 1 through n, in other words 1 × 2 × 3 × ... × (n - 1) × n. When the input is 4, the output should be 24 (because 1 × 2 × 3 × 4 = 24).
) that takes a positive integer n and reports the product of all whole numbers from 1 through n, in other words 1 × 2 × 3 × ... × (n - 1) × n. When the input is 4, the output should be 24 (because 1 × 2 × 3 × 4 = 24).
- Dividing 5! by 4!, the result should be 5
.png) because 5 factorial is really just 5 times 4 factorial. Using your block, check each of these computations—
because 5 factorial is really just 5 times 4 factorial. Using your block, check each of these computations— ,
,  ,
,  and
and  —to see what it reports. One of these is inconsistent with the others. To fix the problem, we need to define 0! = 1. Edit your
—to see what it reports. One of these is inconsistent with the others. To fix the problem, we need to define 0! = 1. Edit your n! block to report 1 if n = 0. Then fully test n! again to make sure it works as it should.
- Debugging: Obviously
 should not work. Check to see what does happen. Then edit your block and find a way to use
should not work. Check to see what does happen. Then edit your block and find a way to use  to check that the input is a number and report some sensible result or message.
to check that the input is a number and report some sensible result or message.
-
Analyzing code: In mathematics, factorial is defined only for positive integers and zero, so 3.7! would make no mathematical sense. But
 reports a result.
Find out what it reports and analyze what the block does so that you can figure out why that is the result.
reports a result.
Find out what it reports and analyze what the block does so that you can figure out why that is the result.
-
Two other mathematical functions:
- Create a block
triangular number n that adds all of the whole numbers from 1 through n:1 + 2 + 3 + \cdots + (n - 1) + n When its input is 4, your block should report 10 (that is, 1 + 2 + 3 + 4). Define your block so that triangular number 0 reports 0.
- Create
 so that
so that  reports the sum 3 + 4 + 5 + 6 + 7, and
reports the sum 3 + 4 + 5 + 6 + 7, and  reports the sum of -3 + -2 + -1 + 0 + 1 + 2 + 3.
reports the sum of -3 + -2 + -1 + 0 + 1 + 2 + 3.
-
Recall that n mod i will tell you if i is a divisor of n.
Counting divisors: Create a block that takes a whole number as input and checks numbers from 1 through that input and counts the ones that evenly divide the input. So, for example, .png) because, from 1 through 8, only the numbers 1, 2, 4, and 8 evenly divide 8.
because, from 1 through 8, only the numbers 1, 2, 4, and 8 evenly divide 8. number-of-divisors 10 should also report 4 because, of the numbers from 1 through 10, only 1, 2, 5, and 10 are divisors of 10. Experiment to find several numbers that have an odd number of divisors.

 does not do what you might expect, because the "ends of the lines" are rounded. Try it.
does not do what you might expect, because the "ends of the lines" are rounded. Try it. .
.


 "Tableau 1" by Piet Mondrian
"Tableau 1" by Piet Mondrian



.png)
 and
and as-letter.png) will help you do that. Experiment with them to see how they work.
will help you do that. Experiment with them to see how they work.-withresult(iboez).png) .
.
 (or
(or  ) that takes a positive integer n and reports the product of all whole numbers from 1 through n, in other words 1 × 2 × 3 × ... × (n - 1) × n. When the input is 4, the output should be 24 (because 1 × 2 × 3 × 4 = 24).
) that takes a positive integer n and reports the product of all whole numbers from 1 through n, in other words 1 × 2 × 3 × ... × (n - 1) × n. When the input is 4, the output should be 24 (because 1 × 2 × 3 × 4 = 24).
.png) because 5 factorial is really just 5 times 4 factorial. Using your block, check each of these computations—
because 5 factorial is really just 5 times 4 factorial. Using your block, check each of these computations— ,
,  ,
,  and
and  —to see what it reports. One of these is inconsistent with the others. To fix the problem, we need to define 0! = 1. Edit your
—to see what it reports. One of these is inconsistent with the others. To fix the problem, we need to define 0! = 1. Edit your  should not work. Check to see what does happen. Then edit your block and find a way to use
should not work. Check to see what does happen. Then edit your block and find a way to use  to check that the input is a number and report some sensible result or message.
to check that the input is a number and report some sensible result or message. reports a result.
Find out what it reports and analyze what the block does so that you can figure out why that is the result.
reports a result.
Find out what it reports and analyze what the block does so that you can figure out why that is the result.
 so that
so that  reports the sum 3 + 4 + 5 + 6 + 7, and
reports the sum 3 + 4 + 5 + 6 + 7, and  reports the sum of -3 + -2 + -1 + 0 + 1 + 2 + 3.
reports the sum of -3 + -2 + -1 + 0 + 1 + 2 + 3..png) because, from 1 through 8, only the numbers 1, 2, 4, and 8 evenly divide 8.
because, from 1 through 8, only the numbers 1, 2, 4, and 8 evenly divide 8. 
(color-0).png)
(color-0).png)
(color-0).png)
(color-50).png)
(color-50).png)
(color-60).png)
(color-60).png)


 and
and  are useful. They are in
are useful. They are in 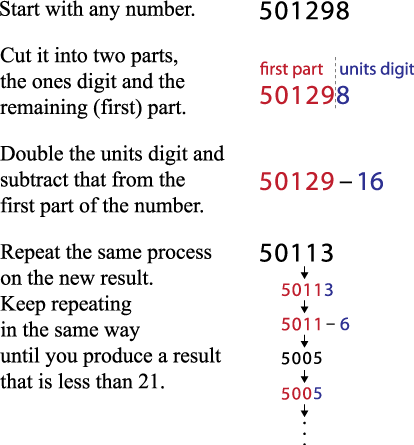
.png)