Interpreting and Displaying GPS Coordinates
-
GH Feedback 1/3/16:
- For you to do is confusing...mix of building some blocks and just asking questions. This could be clarified.
- If there is time: "this" in line 1 is somewhat ambiguous.
- GH Feedback 2/12/16: (From Piazza:) We haven't used STAMP before, so maybe should explain it.
The first GPS coordinates in the Big Burgers data are 40.8,-73.94. GPS coordinates describe a location on Earth by two numbers, a latitude (north-south) and a longitude (east-west).
- GPS coordinates 40.8, -73.94 give a location in New York City. Is the latitude 40.8 north or south? North or south of what?
- The longitude -73.94 indicates New York City is west of longitude 0. How might the longitude of Chicago compare to this number?

Positive values of latitude are north of the Equator, negative values are south. Positive values of longitude are east of the Prime Meridian, negative values are west. The Prime Meridian passes through London.
Searching the Web for GPS coordinates can show the location on a map.
http://www.google.com/#q=40.8,-73.94

- On the map above, give an estimate for where you think 40.8 latitude and -73.95 longitude is located. Then check it. In what direction is this new location, compared to the original?
GPS coordinates are "backwards" compared to the way you've learned in mathematics. In mathematics, and in Snap!, the first coordinate tells you horizontal position, and the second tells you vertical position. GPS coordinates are just different.
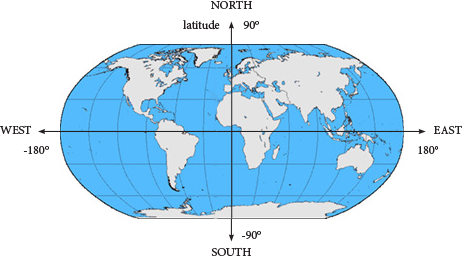
Where is New York on the world map? What are its approximate coordinates?
Original image from Steve Nova at the English language Wikipedia
When you read or write GPS coordinates, the first number is latitude, indicating north-south location, and the second is longitude, measuring east-west. When you use Snap! to plot GPS coordinates, plot them as (longitude, latitude), reversing the written order.
Visualizing the Big Burgers data
It is hard to see much pattern in a list of GPS data; visualizing the data reveals more information.
Transform the data
You can do it your own way instead if you like.
To see the variation in the GPS coordinates, you'll need to transform them. Transforming data and information can lead to new knowledge and new means to communicate it. These problems will lead you through one way to transform the GPS coordinates so you can see them.
Subtracting -74 is the same as adding 74.
- Every point's longitude is around -74 and every point's latitude is around 40.7. This does not help us tell the points apart. Subtract -74 from every longitude and subtract 40.7 from every latitude, using a list operation.
- Replot the data after the transformation. What happens?

- Change your list operation so that, after subtracting, the new values are multiplied by a factor. This is like "zooming in" on the data. Adjust this multiplier and replot until you can see the shape of the data. What does the plot tell you about the GPS information?
Making Snap! do the work is better, because then the program can be used on any set of GPS points in this area, and not just these. That's abstraction.
Build a more general version of this.
- Center the coordinates around the average longitude and latitude. Subtract the average of the longitudes from each one, and do the same for the latitudes. Make Snap! do the work.
- Use multiplication factors so that the data can be properly visualized. How could you use Snap! to automatically determine the multiplication factor?
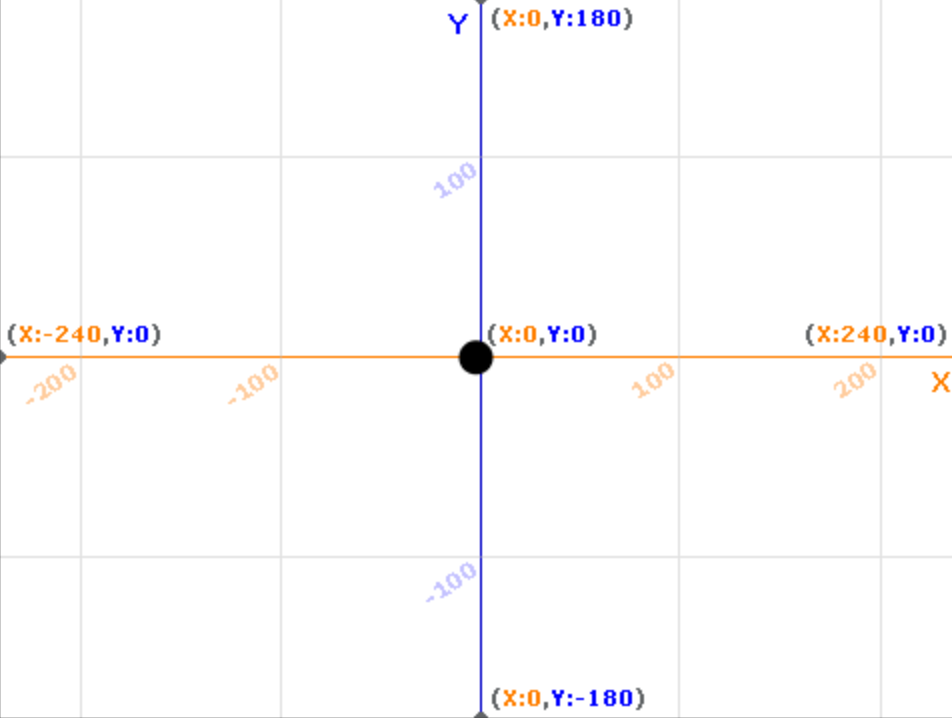 Either add a background and change the sprite costume for your U4L2-GPSData project:
Either add a background and change the sprite costume for your U4L2-GPSData project:
 once to mark the center of the sprite).
once to mark the center of the sprite). Why can't you see all the points?
Why can't you see all the points?

