Analyzing and Improving Searches
- GH Feedback 9/22/15: It would be really helpful if the graphic included the indices of the items in the list. A lot of people fail to make the distinction between between the position and the value.
Alphie: I've got 45 numbers in my recent call list. I'm looking for Gamal's number. I can't remember it, but I'd recognize it if I saw it.
Betsy: Just start at the top and work down.
Alphie: Yeah, but there are so many numbers. It's really hard to find.
Betsy: Did you assign Gamal as a contact? If you did, then just look through your contacts. That's a lot easier, because it's in order.
Alphie: Well, no, it's not in order. I added new people to my contact list when I learned their number. I'll have to sort it some day and change my new contact program to put new numbers where they belong, alphabetically.
Betsy: Oh. Well, then I think the best you can do for now is to write a program that starts at the beginning and looks for Gamal.
Searching Unsorted Data
This approach can become incredibly slow if we're dealing with a lot of data, but is fairly quick when working with short lists.
-
Build a
position of number in unsorted list block that reports the earliest location of a number in an unsorted list or reports "Not In List" (or NIL, if you like) if the number is not in the list.

Searching Sorted Data
Typically, sorted lists are from lowest to highest. You'll create a block that sorts a list of numbers in Unit 7.
If you are searching for a number in a sorted list, you have more information. Suppose you have a sorted list and you want to locate the position of a number.
Alphie: If the list is sorted, we could look at the middle element of the list and see if our number is in the first or last half of the list. That would save time.
Betsy: This feels a lot like the guessing game we built—I pick a number and the computer tries to guess it by splitting the list in half with each guess.
Alphie: But in that one, the computer guessed a number that we picked. Now we want it to find a number and report its position. It should work like this:


Al's note: this should look more like a "kid sketch" and not usable code. BK to MF or anyone else: How do I center an image?? BK to AC: these two images should use the same list; use 9 and not 9.3. BK tech glitch: in building this, when I try to place the sidenote inside the dialog, it cuts out the remaining "span" name callouts. For now the sidenote is outside the dialog box.
Betsy is saying this finder and the number guesser should have the same overall structure.
Betsy: Yes, but it still feels the same. It should have the same guts as the guessing game.
Alphie: OK. Let's modify our guessing game project so that when it gets the number, it tells us how many guesses it took and, instead of saying "Yay" when it finds it, it tells us where the number is in the list.
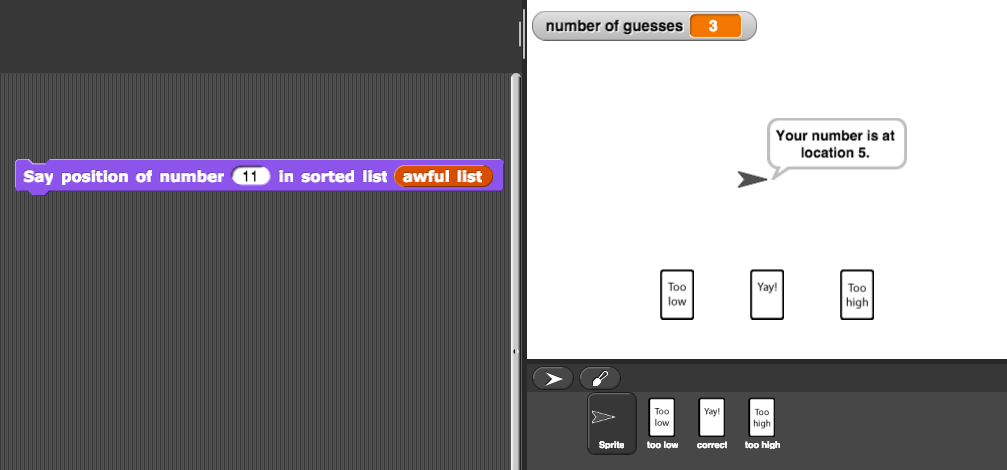
- Implement Alphie's idea: Write a block that says the position of a number in an ordered list and the number of guesses it takes to find it, using the strategy of the guessing game you built on the previous page.
-
Automate your block so that it doesn't have to ask you for feedback. Now, the block should just find the number and say its position:
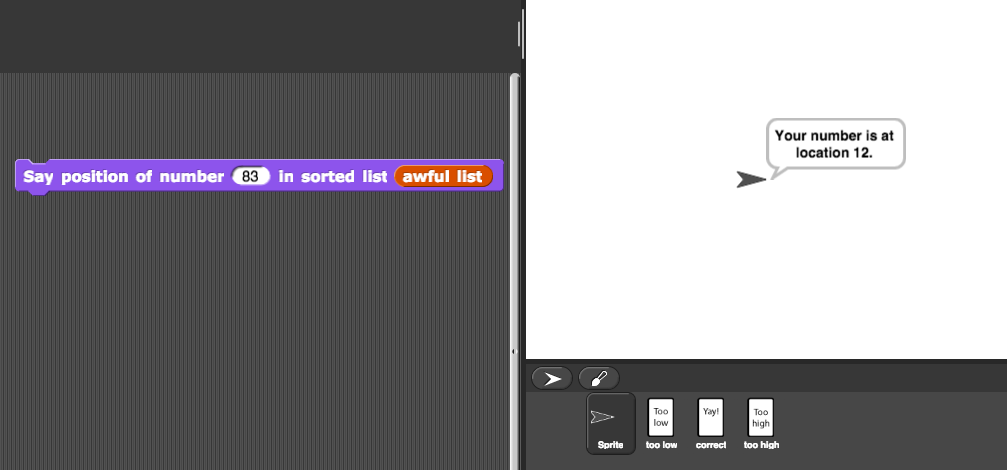
-
Build a
position of number in sorted list block that returns the earliest location of a number in a list sorted from lowest to highest, or zero if the number is not in the list.

Betsy's "it still feels the same" remark is a version of abstraction. She noticed that both the guessing game and the number locator could be built with the same binary search.
-
Make a table that tracks the number of guesses it takes to find the last number in a list as a function of the length of the list:
| Length |
# Of Guesses |
| 3 |
|
| 7 |
3 |
| 15 |
|
| 63 |
|
| 127 |
|
- This type of search is called a binary search. Can you think of some connections to the use of binary in Unit 4?




