

Alan Turing (1912-1954) was one of the founders of computer science. He is known today mainly for two achievements. First, he made a massive contribution to winnng World War II, by inventing a mathematical theory and its implementation in actual hardware to break the secret coded messages generated by the German Enigma coding machine. From 1939 to the end of the war, he was the leader of a secret team at Bletchley Park, England, devoted to breaking Enigma and other German codes. The knowledge of German plans that this gave England was crucial to the Allied victory.
But in this unit it's his second achievement that matters to us. Turing, along with his colleague Alonzo Church, was the founder of theoretical computer science: proving things about how computers must work, regardless of advances in technology. He proved that there are computations that can never be done, no matter how big and fast the computers get.
Keep in mind that when Turing did this work, there were no programmable computers; people had to rewire the parts of the physical machine in order to solve a new problem. Today, with high level programming languages, you can see and understand the essence of Turing's proof much more easily than he could work it out.
By this point in the course you've experienced the frustration of debugging a program. Wouldn't it be great if there were a general-purpose debuging program that could read your code and find all the bugs? Turing proved that this can't be done. In particular, it's not possible to find all infinite loops in a program—situations in which you call a function with a particular input, and the function runs forever, without reporting a value.
Turing used a proof by contradiction, just like Alphie, Betsy, and Gamal on the previous page. They proved that Eve has to be a Truth-teller by assuming the opposite, that she's a False-teller, and showing that that leads to a contradiction.
Similarly, Turing started by assuming he had a predicate function

that takes two inputs, a function and an input value for that function, and reports True if the function would report a value, or False if the function would run forever. (Note that halts? itself can't run forever! We are assuming that it always works, reporting an answer in a finite amount of time.)
Turing then defined this function:
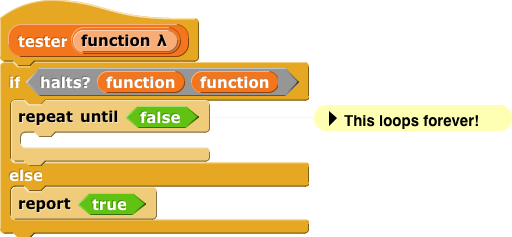
Look at the halts? block in the definition. Turing is asking what happens if we call some function with iteself as its input. This is similar to Betsy making a statement about "this statement" (namely, "this statement is false"). This is easy to do in Snap! because it allows functions as inputs to other functions, as you saw in Unit 3. It wasn't easy for Turing, who had to invent the idea of a computer program that can itself be represented as data inside the computer.
Turing then asked a question that makes the situation exactly like what Betsy said; he calls tester on itself:

If halts? says that tester halts, tester makes sure not to halt! But if halts? says that tester doesn't halt, then tester immediately reports True. (It doesn't actually matter what value tester reports in this case; what's important is that it doesn't loop forever.)
So whatever halts? reported must be wrong. But it's never supposed to make mistakes. So the assumption that we can write halts? has to be wrong! Turing's "halting problem" has been proven to be impossible.
This proof is of practical importance; because of it, nobody tries to write a perfect infinite loop checker. But that's not what mattered to Turing. He just used this example to prove something more general, namely, there are functions that can't be computed. This isn't just a claim about the particular computers that existed in Turing's time, or today. Even when they invent magic quantum hyperspace computers (I have no idea what that phrase would even mean), they still won't be able to solve the halting problem.