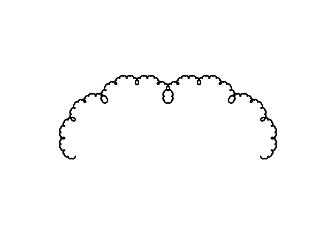
Lévy C-Curve Fractal
Lévy is pronounced lay-VEE.
- GH Feedback 8/4/15: I like this program. I needed Brian Harvey's help to understand the fractal and thus be able to write this program. I know it sounds silly, but the colors threw me off! The base level was red and the next level is a red and blue corner. The next level should be the red and blue corner and then ANOTHER red and blue corner. The coloring messed with my noggin.
- I'm leaving this comment in case we get others like it, but the solution strategy here was not to change the coloring on this page, but to change the coloring on the previous page to match/preview this. That is, I thought this was the best coloring scheme, and that this person was having trouble because the coloring scheme on the previous page appeared to be different. --MF
Another well-known recursive shape is the Lévy C-curve. As in the snowflake algorithm, the base case is a single line segment.

At each level, the algorithm replaces a straight line with a bent line, following this rule: turn 45° left, do the previous level at a reduced size, turn 90° right, do the previous level again, and finally turn 45° left to return to the starting direction. You'll have to figure out how much smaller the size input should be in the recursive calls to make the new level exactly fit the level before.
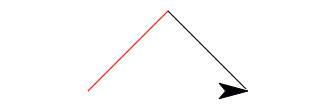
 The original line is replaced by two other lines; together the three would form a right triangle, with the original line being the hypotenuse. If the original line's length is held by the variable size, what length must be passed to the recursive call? That is, what are the lengths of the legs? You can use the Pythagorean formula: a^2 + b^2 = c^2.
The original line is replaced by two other lines; together the three would form a right triangle, with the original line being the hypotenuse. If the original line's length is held by the variable size, what length must be passed to the recursive call? That is, what are the lengths of the legs? You can use the Pythagorean formula: a^2 + b^2 = c^2.
In the third level, the sprite again replaces straight lines with bent lines, drawing 4 smaller lines. Notice that the 2nd and 3rd lines are in the same direction, so when they're the same color, as they will be in your picture, they seem to be one long line.

-
What in the algorithm makes these two lines end up drawn at the same angle?

You may find it helpful to expand this list of commands by writing out the steps within each of the two recursive calls.
Recall, the algorithm for each recursive level is:
- turn 45° left
- recursively call the previous level at the smaller size
- turn 90° right
- recursively call the previous level at the smaller size
- turn 45° left
This simple algorithm builds up a complicated design at higher levels:
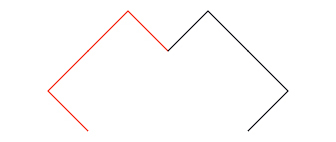

- Develop a program that draws a Lévy C-Curve.
- Changing the angles lets you create interesting variations on the Lévy C-Curve. Try some ideas of your own.