Binary Representation

2.1 A variety of abstractions built upon binary sequences can be used to represent all digital data.
2.1.1 Describe the variety of abstractions used to represent data. [P3]
2.1.1A Digital data is represented by abstractions at different levels.
2.1.1B At the lowest level, all digital data are represented by bits.
2.1.1C At a higher level, bits are grouped to represent abstractions, including but not limited to numbers, characters, and color.
2.1.1D Number bases, including binary, decimal, and hexadecimal, are used to represent and investigate digital data.
2.1.1E At one of the lowest levels of abstraction, digital data is represented in binary (base 2) using only combinations of the digits zero and one.

While people typically work with numbers using the base 10 (decimal) numeral system, other systems are relevant in computer science, including binary (base 2) and hexadecimal (base 16). Computers manage data packed as sequences of bits (binary digits), which are all zeros or ones. People are most familiar with base 10, so we write software that allows people to use base 10 to communicate with the computer.

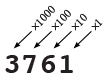
In base 10, there are ten digits (0-9), and each place is worth ten times the place to its right.
place values in decimal

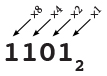
In binary, base 2, there are only two digits (0 and 1), and each place is worth two times the place to its right.

The subscript 2 on 11012 means the 1101 is in base 2. Numbers are normally written in base 10, so a subscript 10 is only used when needed for clarity.
place values in binary

  1. Talk with Your Partner Watch this Binary Timer Snap! program run. Write a description of the binary counter's behavior. Explain what you see going on.
    binary coutner Snap! project

Reading Binary

In base 10 notation, each place value represents a power of ten: the units place (100 = 1), the tens place (101 = 10), the hundreds place (102 = 100), the thousands place (103 = 1000), etc. So, for example:

9827   =   9 × 103  +  8 × 102  +  2 × 101  +  7 × 100

place values in binary Base 2 uses the same idea but with powers of two instead of powers of ten. Binary place values represent the units place (20 = 1), the twos place (21 = 2), the fours place (22 = 4), the eights place (23 = 8), the sixteens place (24 = 16), etc. So, for example:

100102   =   1 × 24  +  0 × 23  +  0 × 22  +  1 × 21  +  0 × 20   =   16  +  2   =   1810

Here's a video from a different version of BJC. It cuts off just before talking about base 16. (You'll see more about reading hexadecimal soon.)
Set Up Your Headphones or Speakers

If your connection blocks YouTube, watch the video here, but you only need to watch the first 3:10—up to (but not including) the part about hexadecimal.
There is a mistake in the video at 2:50. Do you see why? (Also, not everyone learns base 10 place values in kindergarten!)

To translate from binary (like 101101_2) to base 10, first, write the number out on paper. Then write out the binary place values by doubling left from the units place:

1011012 has only six digits, so we don't need powers of two to the left of that.
1 0 1 1 0 1
32 16 8 4 2 1
right-to-left arrow

This means this number is 32 + 8 + 4 + 1. So, 101101_2 = 45_{10}.

  1. Translate these binary numerals into base 10 notation:
    1. 1012
    2. 1112
    3. 10100112

Writing Binary

To translate from base 10 (like 89_{10}) to base 2, first write out the binary place values by doubling left from the units place until you get to a value larger than your number (256 for this example). Then think, "My number is smaller than 128, so I can leave that place blank. But I can take out a 64, so I write a 1 there, and there's 25 left (89 – 64). I have 0 thirty-twos, because I only have 25. But I can take out 16, and there's 9 left. So, 8 and 1 are the last nonzero bits.

Either way you are converting (and between any bases), always write the place values right-to-left (just like with units, tens, hundreds, etc.), and always write the number itself left-to-right (just like normal).
89
25
9
1
0
right-to-left arrow
128 64 32 16 8 4 2 1
  1 0 1 1 0 0 1

Now, read the number off: 1011001_2=89_{10}.

Here's another video. (It also cuts off before talking about base 16.)

If your connection blocks YouTube, watch the video here, but you only need to watch the first 3:14—up to (but not including) the part about hexadecimal.
Set Up Your Headphones or Speakers
Here's an algorithm you can follow to find the base 2 representation of any base 10 integer:
    You'll learn about how other real numbers are stored soon.
  1. First, find the largest power of two that fits inside the number.
  2. Then, subtract that power of 2 from the number, keep the new number, and record a 1 in the place for that power of 2.
    3. You could create a program based on an algorithm like this.
    There is another method and another explanation of this method described on wikihow.com.
  3. Then, determine if the next largest power of 2 fits inside the new number, and:
    • If it does, subtract that power of 2 from the number, keep the new number, and record a 1 in the place for that power of 2.
    • If it doesn't, keep the same number, and record a 0 for that power of 2.
    Repeat this whole step with the next largest power of 2 until you have a bit (1 or 0) for all the remaining places down to and including the ones place (by which point you should have nothing left of the original number).

The string of ones and zeros you have recorded is the binary representation of your original number.

  1. Represent these base 10 numerals in binary (base 2):
    1. 63
    2. 64
    3. 65
    4. 129
    5. 128
    6. 127