-
 Watch this Hexadecimal and Binary Timer Snap! program run. The top row counts in binary, the middle in decimal, the bottom in hex. Write a description of the hex counter's behavior.
Watch this Hexadecimal and Binary Timer Snap! program run. The top row counts in binary, the middle in decimal, the bottom in hex. Write a description of the hex counter's behavior.
Typing long strings of ones and zeros is inconvenient very prone to error. One common compromise is to use hexadecimal (base 16). Four binary digits represent the values 0 through 15, whereas only one hex digit also represents 0 through 15. So eight digits of binary can be translated into two digits of hexadecimal, which is much easier and much less error-prone for humans.
| Eight bits in base two... | |||||||||||
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | ||||
| 128s place | 64s place | 32s place | 16s place | eights place | fours place | twos place | ones place | ||||
| ...is two digits in base 16. | |||||||||||
| 161 | 160 | ||||||||||
| sixteens place | ones place | ||||||||||
| For example: 12110 = 011110012 = 7916 | |||||||
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 7 | 9 | ||||||
| 10 | 11 | 12 | 13 | 14 | 15 |
| A | B | C | D | E | F |
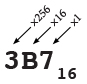
.jpg) Base 16 uses powers of sixteen instead of powers of two or ten. Place values in hexadecimal represent the units place (160 = 1), the sixteens place (161 = 16), the two hundred fifty-sixes place (162 = 256), the four thousand ninety-sixes place (163 = 4096), etc. So, for example:
Base 16 uses powers of sixteen instead of powers of two or ten. Place values in hexadecimal represent the units place (160 = 1), the sixteens place (161 = 16), the two hundred fifty-sixes place (162 = 256), the four thousand ninety-sixes place (163 = 4096), etc. So, for example:
3B16 = 3 × 161 + 11 × 160 = 48 + 11 = 5910
This video continues one you saw before.
To translate from hexadecmial (like 7B3_{16}) to base 10, first, write the digits on paper. Then write out the hexadecimal place values: start at the right with 1, then write 16 in the next place to the left, then write 256 (which is 162), and so on. Each new place will be worth 16 times the one to its right.
| 10 | 11 | 12 | 13 | 14 | 15 |
| A | B | C | D | E | F |
| 7 | B | 3 |
| 256 | 16 | 1 |

|
||
This means 7B3_{16} = 7 \cdot 256 + 11 \cdot 16 + 3 \cdot 1 = 1792 + 176 + 3 = 1971_{10}.
To translate from base 10 (like 299_{10}) to base 16, first write out the hex place values by multiplying by 16 moving left from the units place until you get to a value larger than your number (4096 for this example). Then think, "My number is smaller than 4096, so I leave that place blank. But I can subtract a two hundred fifty-six once, so I write a 1 there, and there's 43 left. Now, I can subtract 2 sixteens, and there's 11 left. And 11 is B in hex.
| 0 |

|
|||
| 4096 | 256 | 16 | 1 |
| 1 | 2 | 11 (B) | |
Now, read the number off: 12\text{B}_{16}=299_{10}.