(Recall that the floor() function rounds a number down to the closest integer.)
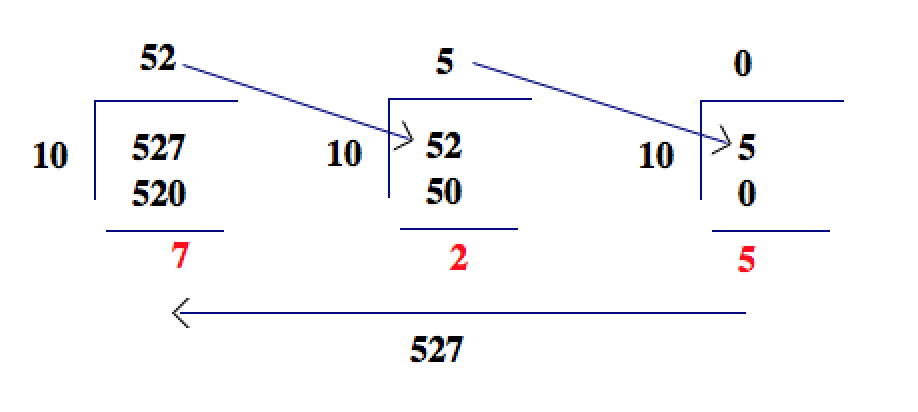
First a reminder how to extract each digit in base 10 system.
Example: If you were trying to extract the digits of a number, say, 527 in base 10, you would take the following steps.

(Recall that the floor() function rounds a number down to the closest integer.)
This is where we stop. So 527= 5(100) + 2(10) + 7(1)
Note with the algorithm we extracted the digits right to left. (7 first, 2 next, 5 last)
Example: If you apply a similar procedure to get the binary representation of a number, say, 25, you would take the following steps.
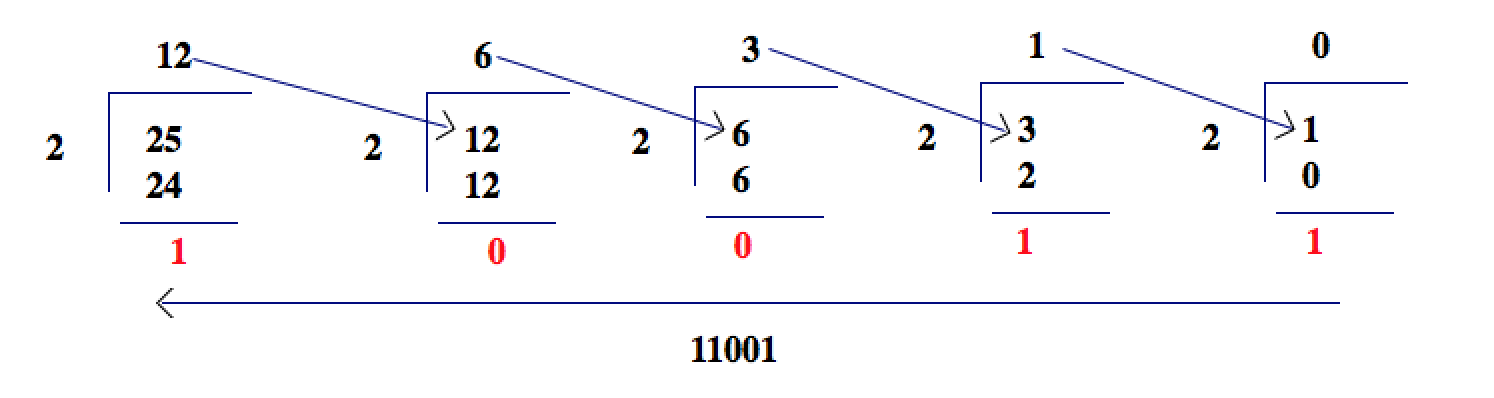
This is where we stop. Note with the algorithm again we extracted the digits right to left.
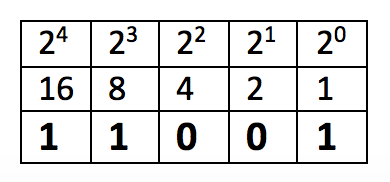
So 25= 1(16) + 1(8)+ 0(4) + 0(2) + 1(1) = (11001)2
Using these examples come up with an algorithm to represent any base 10 number in base 2.
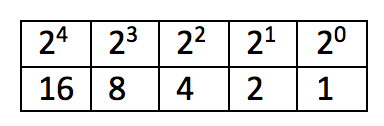
Is 24 =16 contained in 25? Yes, write 1. 25-16=9 Is 23 = 8 contained in 9? Yes, write 1. 9-8=1 Is 22 = 4 contained in 1? No, write 0. Is 21 = 2 contained in 1? No, write 0. Is 20 = 1 contained in 1? Yes, write 1. 1-1=0 Done.