Comparing Algorithms

EK: 4.1.1H, 4.1.1I, 4.2.4D
This introductory box is a new design feature that the BJC development team is considering using throughout the student lab pages. Its goal is to help students anticipate what they will be working on.
Is it helpful to you? How could we make it better? Please use the blue feedback button at the bottom to support BJC with your ideas!

In this lab, you will learn that some ways to solve a problem are faster than others.

On this page, you will compare two algorithms for adding all numbers from 1 to an input number and figure out which is faster.

Alphie and Betsy are creating algorithms that take a positive integer as input and report the sum of all integers from 1 to the input number, like this:

Their two different approaches always give the same outputs for the same inputs. Alphie and Betsy are discussing their different approaches.
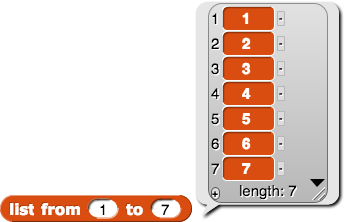
Alphie: I made two new blocks. First, I created a reporter to list of all the integers between and including two integers, and then I used combine to add up the list.
Alphie shows his work:

Betsy: Great! I think we can do it another way too.
Alphie: Cool. How?
Betsy: I was thinking about adding, and I noticed that 1 + 13 = 14 and 2 + 12 = 14 and 3 + 11 = 14...
Alphie: So, you added up fourteens?
Betsy: Yeah. I wrote down the list from 1 to 13 and then I wrote the same numbers in reverse order—right under my first list, like this:
Betsy writes on the board:
1 2 3 4 5 6 7 8 9 10 11 12 13
13 12 11 10 9 8 7 6 5 4 3 2 1
Betsy: Then I added down and got thirteen fourteens:
1 2 3 4 5 6 7 8 9 10 11 12 13
+ 13 12 11 10 9 8 7 6 5 4 3 2 1
14 14 14 14 14 14 14 14 14 14 14 14 14
Betsy: And 13 times 14 is 182...
Alphie: But the answer is 91.
Betsy: Right. I added each number in twice, so the answer is half of 182, which is 91.
Betsy writes \frac{13 \times 14}{2}=91.
Alphie: Oh, and if you wanted to add the numbers from 1 to 50, you'd multiply 50 and 51 and divide by 2 to get (Alphie calculates) 1275.
Alphie writes \frac{50 \times 51}{2}=1275.
Betsy: (smiling) So in general to add the numbers between 1 and some number, n, you multiply the input number by one more than the input number and then you divide the result by 2...
Betsy writes \frac{n \times (n + 1)}{2}.
Then Betsy builds the block, and Alphie helps debug.
  1. Discuss these two algorithms and make a hypothesis: Which algorithm do you think will be more efficient? Why?
  2. Implement a sum from 1 algorithm. You can use Alphie’s method (using combine to code sum), you can use Betsy’s formula, or you can build it your own way.
    For Alphie’s method, you’ll need to code too.
    "U5L3-ReporterTimer"Save your work as U5L3-ReporterTimer
  3. Work with another team to compare Alphie's and Betsy's algorithms across a variety of inputs. Determine which is more efficient.
  4. Consider what makes that algorithm more efficient. Write or share your thoughts.
  1. If you built a graphing app, try plotting y= sum from 1 to( x).