Remix Your Pinwheel

Ruthless Suggestions from Al

Teacher feedback from 2017-2018: one teacher: "On page 5 the picture of the asterisk does not look like what their output should be, it should be all one color and all equally spaced. This really confused all students. On page 7 the rectangle block. My students were able to do this but most of them did not use loops here. This would be a great opportunity for them to get a better understand of the importance of loops and see if we can challenge them to write a loop or have them trace a rectangle on paper and see how many times they repeat. This is what I did with my students. Students had a lot of problems understanding parameters I did a mini lesson on this. This might be something we might want to go into more examples and explanations of. The quick blurb about the definition did not get them the understanding they needed." --MF, 3/6/19

PG: Why is "remix" a useful, or even appropriate term here? Edit? Modify?

It comes from Scratch by way of Selim. But Scratch uses it to mean modifying someone else's project, which is also what it means in its original context of music. -bh

On this page, you will use your existing pinwheel block to make asterisk and polygon blocks.
Animation cycle from Asterisk to Polygon

You can use your general-purpose pinwheel procedure to create other, simpler special-purpose procedures that each do a particular job.

Asterisk with 12 branches
  1. If it isn't open already, open your U1L3-Pinwheel project from the previous page.
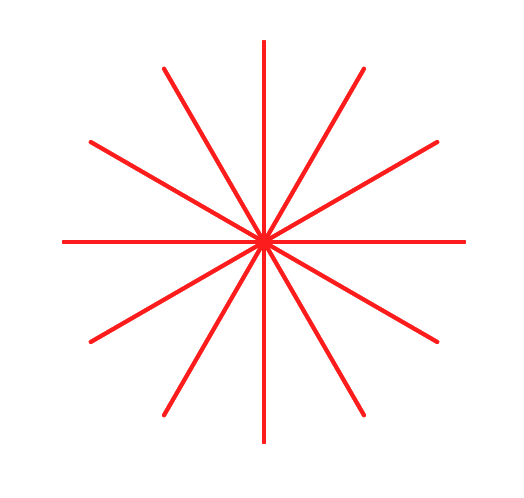
  2. Use your pinwheel block to create a more specialized asterisk block.
    1. First, make a new block called asterisk with two inputs: one for the number of branches and one for the length of each branch. You may wish to review how to make a new block at Unit 1 Lab 2 Page 4: Making Your Own Block.
      2. asterisk, branches:(branches) branch length:(length){pinwheel, branches: ( ) size:( ) backup:( )}
    2. Now fill in the three inputs to pinwheel so that it correctly draws an asterisk.
Pair Programming Swap
  1. Similarly, write a polygon block that uses pinwheel with appropriate inputs to draw a polygon with a given number of sides and side length.

On page Unit 1 Lab 2 Page 2: Making Programs Talk, you learned about procedural abstraction: giving a code segment a name (making it a block). That way you can call it more than once instead of copying and pasting.

Mary, please fix CSS so that <code> comes out with style="color: #f0f" and something for var and also side/endnotes come out color:black.
AAP-3.B.4

Here is another kind of abstraction: noticing that asterisk and polygon are both kinds of pinwheels, and writing one, more general, pinwheel block that uses an input so that the block can be used to make asterisks, polygons, or other interesting designs.

AAP-3.B.5

This is an example of abstraction by generalization: looking at chunks of code that are almost the same and writing a single block by using an input to distinguish among the different cases.

  1. If you look inside of pinwheel and see how you're using it in polygon, you'll see that there are steps that you don't really need for the case of a polygon. Write another version of polygon built directly out of primitive blocks (move, turn and so on). How simple can you make it?
    2. AAP-3.B.7
    As long as your polygon block draws the right picture, it doesn't matter to the rest of the project what's inside it.
Save your work
  1. Use your pinwheel block code one last time to create a circle block that accepts one input for the size.
  2. Use the random block together with set pen color and set pen size to draw a variety of shapes.
    assortment of pinwheels
  1. Challenge: Create a script that draws a blue square of size 100 and then draws a red circle that fits perfectly inside it.
    red circle in blue square
  2. In each of the puzzles below you will need to write code that will allow a car to travel from its starting point (A) to its final destination. Click on each of the images to load each Snap! project.
    Triangle and square tesselation path Triangle, square and hexagon tesselation path Octagon and square tesselation path