The Base Case

Tim points out that we are missing an "On this page" here. --MF, 5/23/20

PG: Change. I also really dispute leading people down the garden path. This is a common error, but we should not mandate it. If we're going to be didactic, we should not didact in the wrong direction.

I agree with Paul. This is not good pedagogy. I'd be find to have Alpha, Betsy, and Gamal run into and discuss this bug, but it's not ok to handhold kids into doing the wrong thing. --MF, 4/3/19

A script that contains itself is recursive .

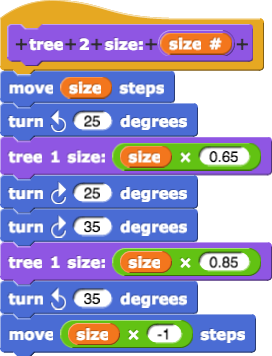
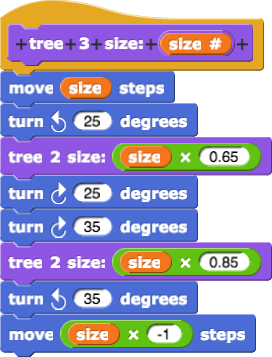
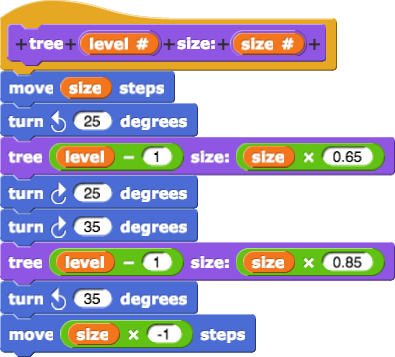
It seemed to make sense to replace all the look-alike numbered tree scripts with a single recursive script with the same structure:
tree2 size:(size#){move(size) steps; turn counterclockwise (25) degrees; tree 1 size:(size*0.65); turn clockwise(25) degrees; turn clockwise(35) degrees; tree 1 size:(size*0.85); turn counterclockwise (35); move(-1*size) steps}  tree 3 size:(size#){move(size) steps; turn counterclockwise (25) degrees; tree 2 size:(size*0.65); turn clockwise(25) degrees; turn clockwise(35) degrees; tree 2 size:(size*0.85); turn counterclockwise (35); move(-1*size) steps}       ...        tree level:(level#) size:(size#){move(size) steps; turn counterclockwise (25) degrees; tree level:(level-1) size:(size*0.65); turn clockwise(25) degrees; turn clockwise(35) degrees; tree level:(level-1) size:(size*0.85); turn counterclockwise (35); move(-1*size) steps}

But it didn't work:
Tree drawing never terminates, stuck at a single branch

Betsy: Aaarghhh! What's going wrong?!!
Alphie: It never stops!
Gamal: After it turns to the left, it should make a smaller tree, but then it's supposed to finish and turn to the right and do a tree, there, too.
Betsy: Oh, right, Gamal! It's not going right!
Gamal: Yeah, in each recursive call to tree, the sprite draws smaller and smaller left branches until it seems to be just spinning around in one place. It never draws a right branch to finish the tree it's working on.
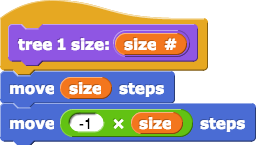
Alphie: I get it. The original numbered tree 1, tree 2, etc. blocks aren't all the same. The first one, tree 1, is different; it just draws a line, no branches, and puts the sprite back where it started.

Alphie points to the tree 1 code and to the figure it draws.
tree 1 size:(size#){move(size) steps; move(-1*size) steps} tree1 result: Trunk of tree drawn

Betsy: So our recursive tree block has to do something different when the level = 1!
Gamal: Yup! It has to draw just a line without adding another branch.
This different version for the lowest level of a recursive script is called the base case.
Betsy: Let's think through a simple tree to figure out how this "base case" needs to work. Let's look at tree 3 with size 40.
tree 3 size:(size#){move(size) steps; turn counterclockwise (25) degrees; tree 2 size:(size*0.65); turn clockwise(25) degrees; turn clockwise(35) degrees; tree 2 size:(size*0.85); turn counterclockwise (35); move(-1*size) steps} clear; point in direction (0); pen down; tree 3 size:(40)
Alphie: Ok, after clearing the stage, pointing up, and putting the pen down, the sprite will move 40 steps and then turn 25° left. And then it will call tree 2 with a smaller size.
Betsy: Right. And tree 2, which is almost the same, will move, turn, and then call tree 1, which just draws a line and goes back. Then, tree 2 tells the sprite to turn right 60° and draw another little tree 1 and....
Gamal: Yeah, and because tree 1 finishes, that lets tree 2 finish! So, it'll look like this when tree 2 finishes: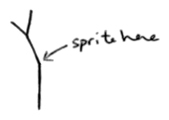
drawing of tree 3 after the first tree 2 is called
Alphie: Yup. And then the tree 3 script turns right 60° and uses the whole tree 2 script again to create the other side. Then it'll turn back 35° and move backwards to the very beginning.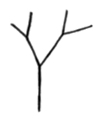
drawing of tree3 after the second tree 2 is called
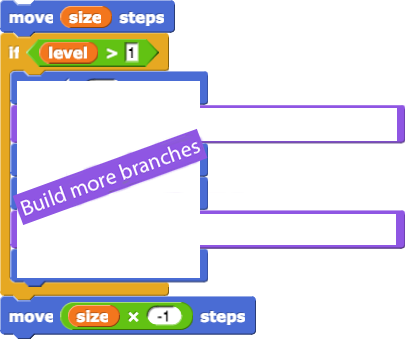
Betsy: So that's how tree 3 finishes. Now, about that "base case" thing for the recursive tree script... The base case is the lowest level of the recursion, so that's like the tree 1.
Alphie: Yeah, the tree 1 just draws a line and doesn't try to make another tree.
Betsy: So, we need our recursive tree block to draw a line at level 1 instead of making more little trees forever.
  1. Correct your recursive tree block so it includes a base case to stop the script from calling itself forever. Here are two ways you could do that, and there are more. Use whatever makes most sense to you.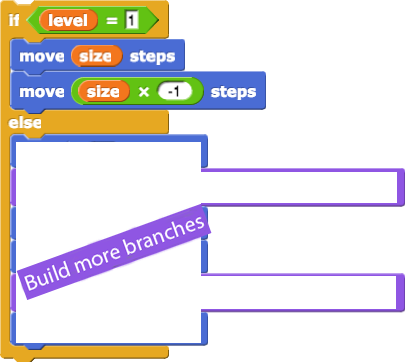
    if(level=1){move(size) steps; move(-1*size) steps}else{...Build more branches...}               move(size) steps; if(level>1){...Build more branches...}; move(-1*size) steps
  2. Run tree level: 9 size: 50. If it is now working properly, you should get a result like this: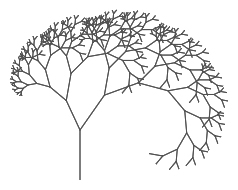
    Tree with trunk and 8 levels of branches
  3. The time it takes to draw the tree increases very quickly with the number of levels, so we don't recommend trying 20 levels. But try timing level 8 through level 12.
  1. Analyze: tree 1 produces just one stick. How many new sticks (branches) are produced by tree 2? Then, how many new ones are produced by tree 3? By tree 4? Figure out how many new twigs are added at level 10. You can now see why it would take a long time to draw level 20.
Take turns speaking

Recursive scripts call themselves. In order for them to stop, there must be some special case when they don't call themselves. We call that the base case, a simpler version of the script that doesn't call the block itself.

There is usually a conditional (like if-else) with two cases: a base case for the lowest level that stops the recursion from going on forever and a recursive case that calls the script itself again and again at lower levels until it reaches the base case.

When a script does keep recursively calling itself forever (as when the sprite was just spinning around in one place), that's a bug, and we say the program is stuck in an infinite loop.

  1. Add a global count variable, incremented first thing in the tree block, to record the number of times that tree is called when running different levels. Make a table. What pattern do you find?
    level count
    1 1
    2 3
    3 7
    4 ?
    5  
    6  
    etc. etc.
    2. This is an example of exponential growth. This kind of growth for an algorithm is considered to take unreasonable time as you saw in Unit 5 Lab 3: Classifying Algorithms. This is why we suggested against trying 20 levels.