Unit 7 Lab 2 Teacher Guide

In this lab, students explore more variety in fractal shape generation and practice writing recursive definitions (like tree in Lab 1) right away without first constructing non-recursive versions (e.g. tree 1, tree 2, tree 3, etc.) of their programs. Students explore several common fractal structures, see how fractal structures occur in the natural world, and then use recursion to model the artwork of Mondrian.

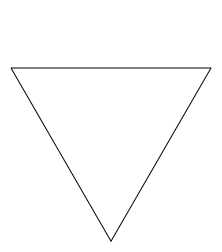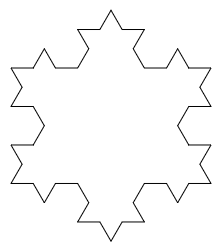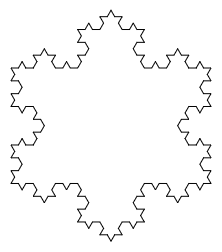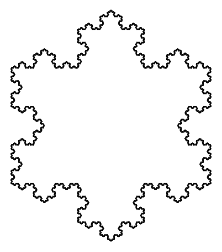
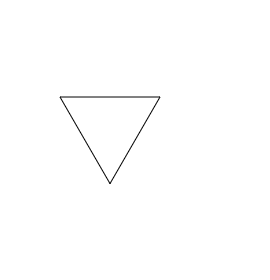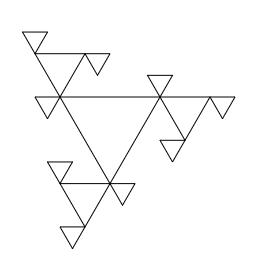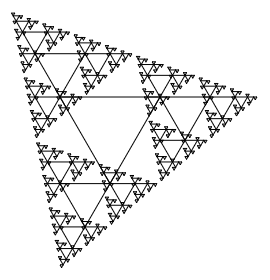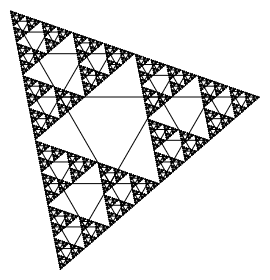Page 1: Triangle Fractal.
- Learning Goal: Practice recursion by developing several fractal-drawing programs.
- Debugging: Triangle
  - This optional debugging activity is similar to one that students saw in Unit 1 with a pentagon. The purpose is to highlight the difference between the interior angle of a polygon and the turning angle that a sprite must move through in order to create each angle of the shape. Use as needed with your students. Additional details on clarifying this idea are included in the "Tips" section below.
- Tip: You may need to remind students of the difference between an interior angle (like the angles they learn about in math class) and an angle of sprite rotation (exterior angle). Students associate the angles of a equilateral triangle are 60° but, to draw a triangle with a sprite, they need to think how the sprite turns. After drawing each side, note the direction the sprite is facing; it must turn 120° in order to draw the next side. Demonstrating this to students by using a physical object (e.g., a pencil) to represent the sprite as it moves may help.
Page 2: Koch Snowflake.
- Learning Goal: Practice recursion by developing several fractal-drawing programs.
- Discussion: Discuss the last "For You To Do" question as a class: Why does the size in each recursive call have to be one third the size of the previous level? There are four copies; why not one fourth the size?
Page 3: Lévy C-Curve Fractal.
- Learning Goal: Apply mathematics (including Pythagorean formula, coordinate positioning, and angles) to computer graphics.
- Discussion: After students have had time to explore them on their own, you may want the class to discuss the first two questions (about the size input for the recursive calls and about how the turning angles combine to create a 180° angle).
- Tip: Students may require some support around the use of the Pythagorean formula on this page, but it is not beyond an introductory algebra student. Since size is the length of the long side of an isosceles right triangle, the size of the smaller sides can be found in this way:
  $smaller^2 + smaller^2 = size^2$ $2 \times smaller^2 = size^2$ $smaller^2 = \frac{size^2}{2}$ $smaller = \sqrt{\frac{size^2}{2}}$ $smaller = \frac{size}{\sqrt{2}}$
Page 4: Recursive Mondrian.
- Learning Goal: Use recursion to create Mondrian-style pictures.
- Debugging: Mondrian Base Case
  - The script presented asks students to take a careful look at a bug with coordinate positioning and state transparency. Instead of undoing the moves done by rectangle, the buggy script attempts to return the sprite by placing it at $(\frac{width}{2},\frac{height}{2})$ . This would work for the base case as it is centered around the origin. However, the rectangles in Mondrian are generally not centered around the origin, and so the script does not produce the intended image.
- Tips:
  - Sorting out the correct inputs for all of the missing slots in the recursive script requires thought. You may want to talk some things through as a class after students have had a chance to try it on their own for a bit.
    $Mondrian level: (level) width: (width) height: (height){if (level=1){rectangle width: (width) height: (height)} else{script variables (fraction); set(fraction) to ((pick random (1) to (4))/5); if (width>height){Mondrian level:() width:() height:(); change x by (); Mondrian level:() width:() height:(); change x by ()} else{Mondrian level:() width:() height:(); change y by (); Mondrian level:() width:() height:(); change y by ()}}}$
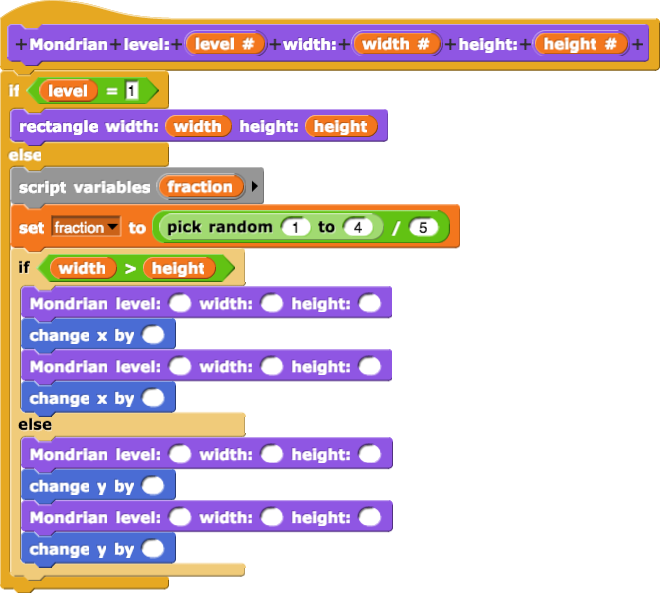
  - Encourage students to work on the empty blocks in Mondrian one at a time. For example, students can completely ignore what happens when height > width by setting the input level for the initial call to Mondrian to 2 and just focusing on getting level 2 to work first. In fact, they can even focus just on the very first recursive call within Mondrian and getting the right-most level 2 rectangle working first, like this image below:
    
    After getting level 2 to work correctly, they can follow a similar block-by-block process with level 3: getting the upper-right-most level 3 rectangle working with the first recursive call to Mondrian within the else case of the if-else block:
  - We opted to provide much of the structure of this program, but it's still a complex project to consider. If possible, encourage students to at least read the list of considerations for the recursive Mondrian block before the end of the first class period on this lab. You may also want to read the list as a class at the beginning of the second day on this lab and have students indicate where these ideas appear in the script and share their thoughts or observations with the class.

Lab 2: Recursion Projects

Pacing

Prepare

Lab Pages

Related Resources:

Solutions