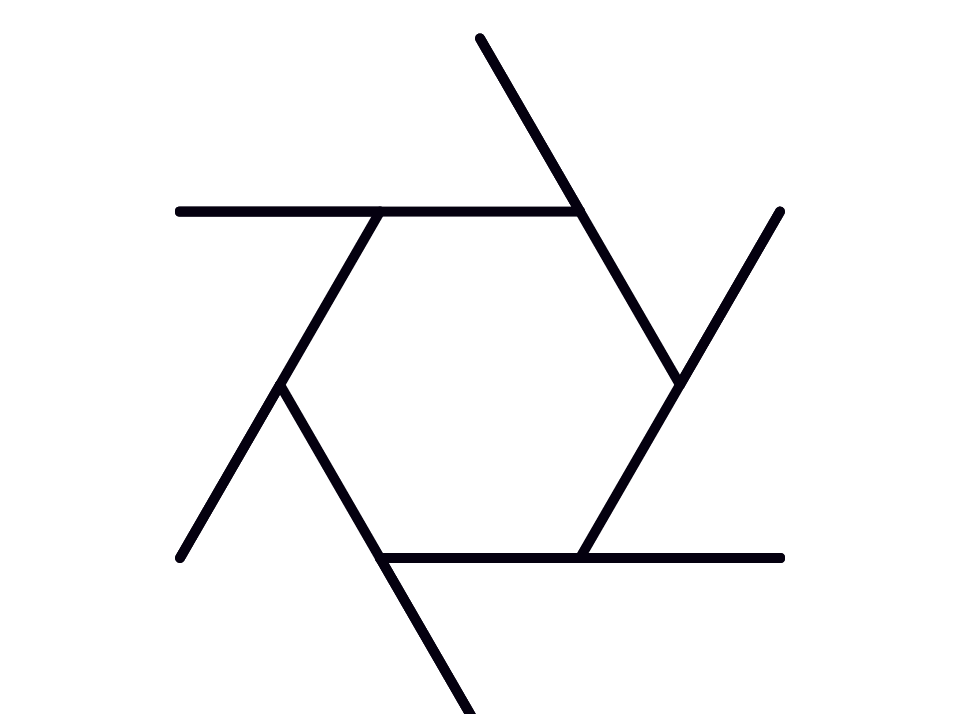Polygonal Racetracks
In this project, you are going to explore the turning angles needed to trace or draw regular polygons.
A regular polygon is a geometric figure in which all the sides and angles are equal.
Imagine that you have a racecar that needs to travel on a racetrack in the shape of a regular polygon. Every time the car reaches a corner, it needs to make a turn in order to stay on track. But, how much is this turn? And exactly how does it depend on the number of sides of the polygon?
- Use this interactive program to see demonstrations of how the racecar would travel in such a track.
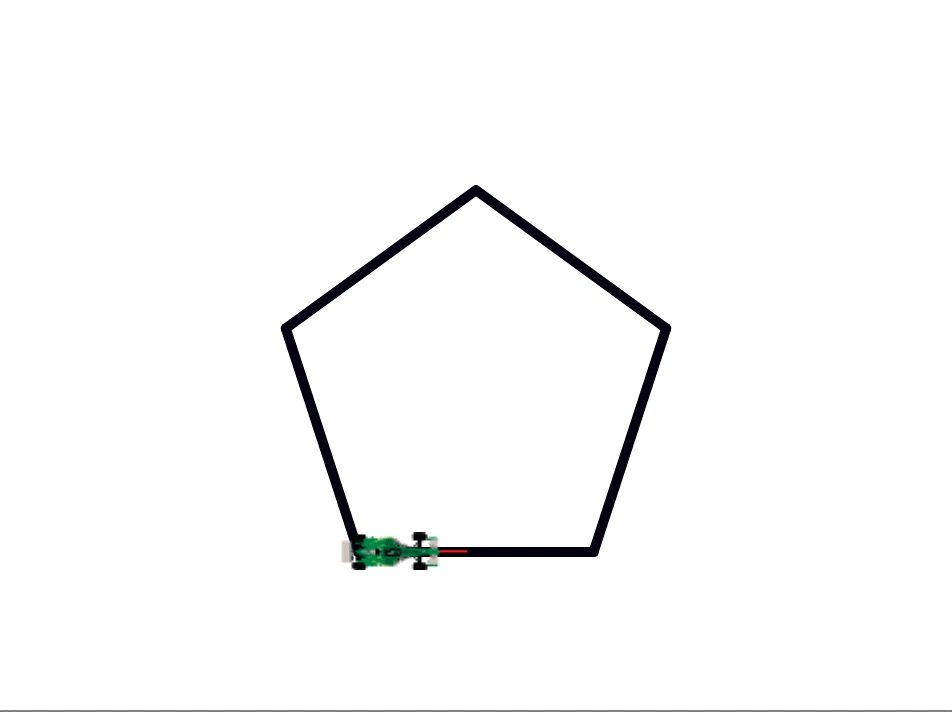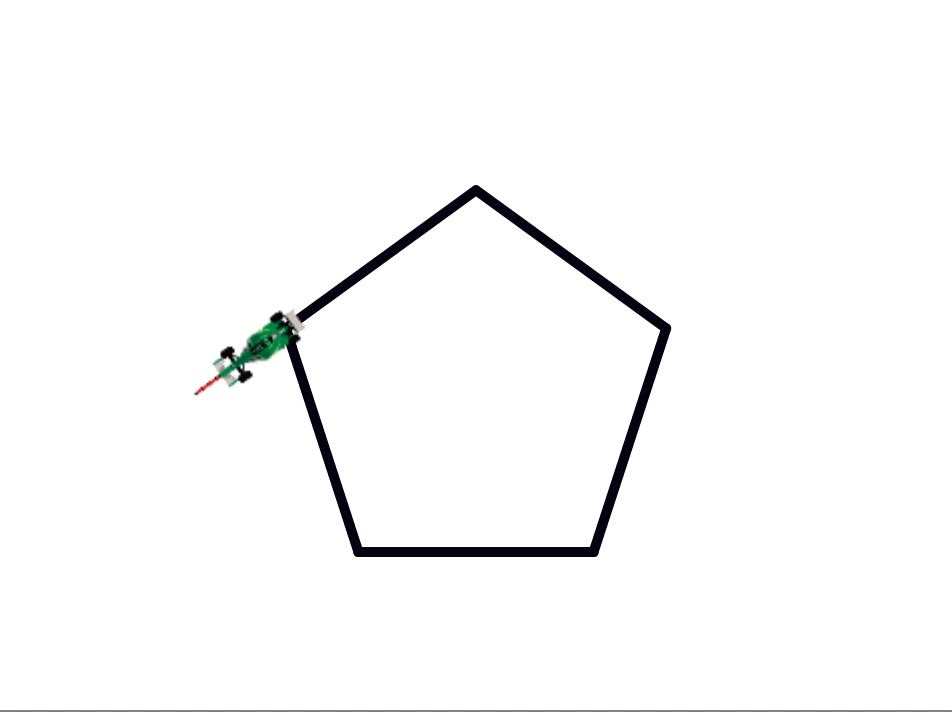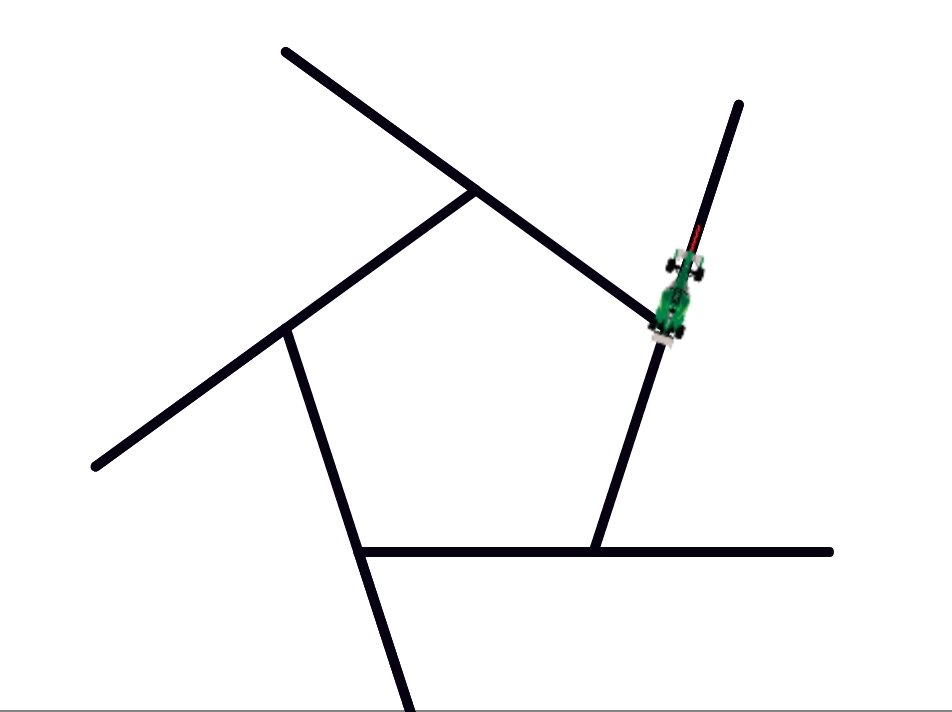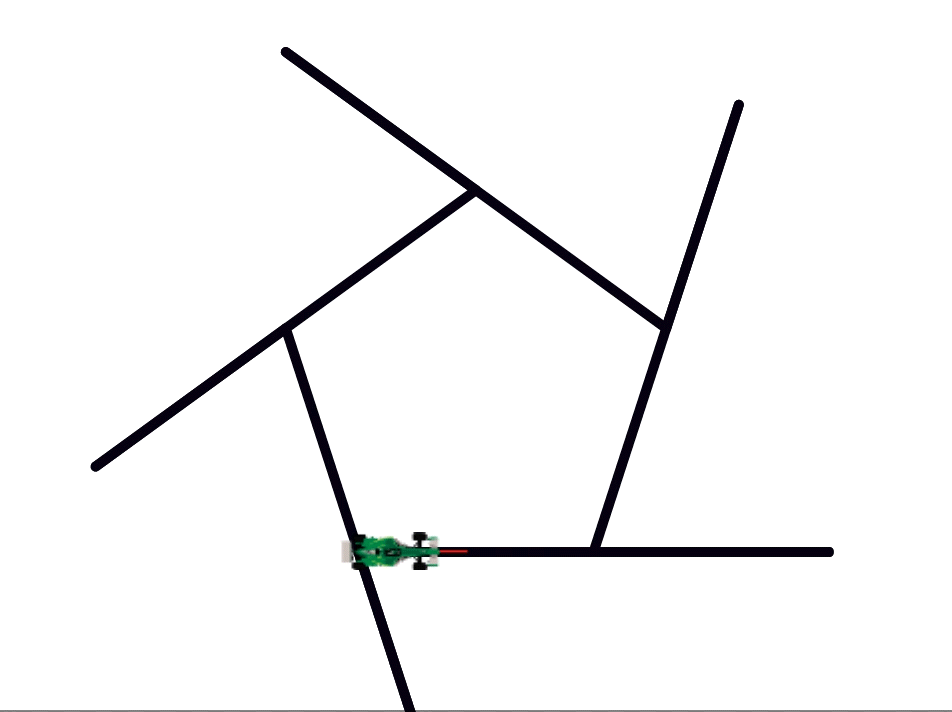
Notice in the movie below that (unlike what intuition might say) the turning is done not inside but outside of the polygon.
![Triangluar racetrack turning angle tracing Triangluar racetrack turning angle tracing]()
Now you will discover what the turning angle must be for each of the polygons below:
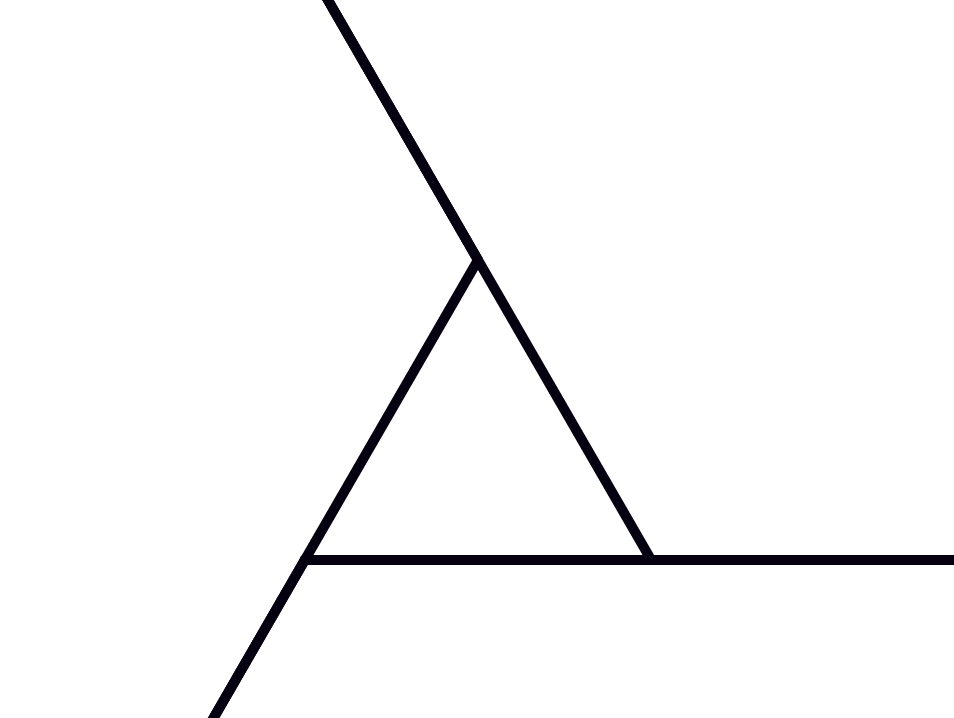
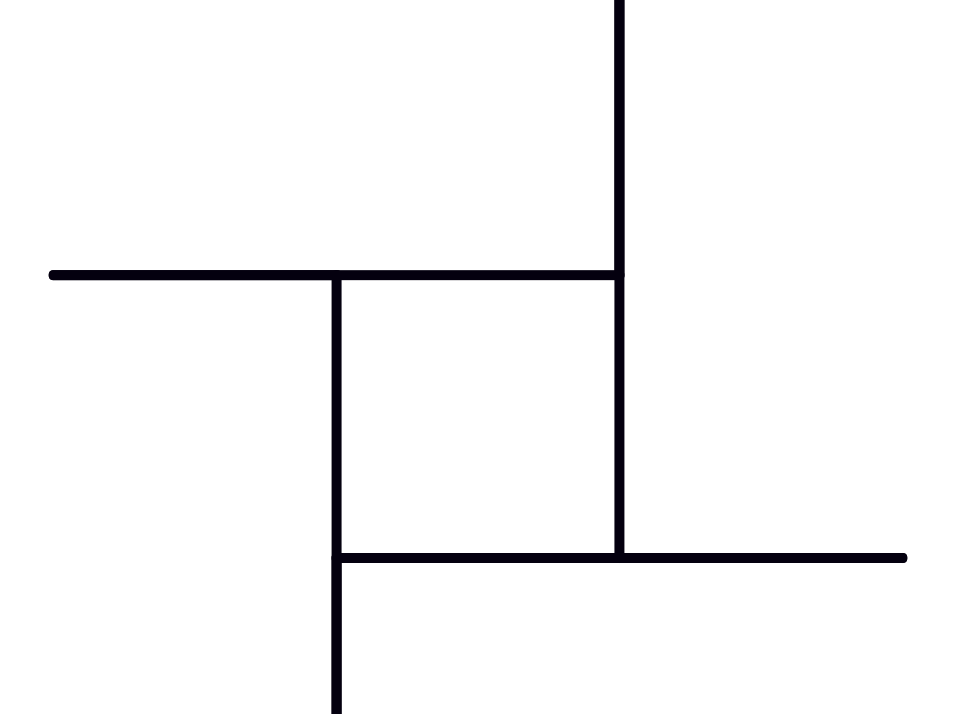
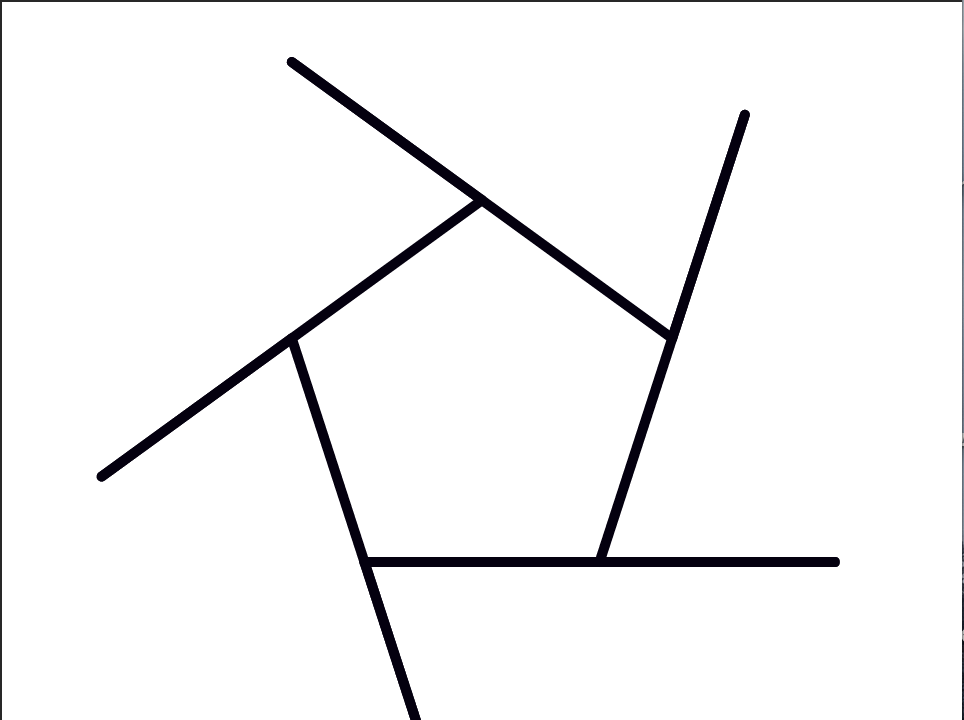
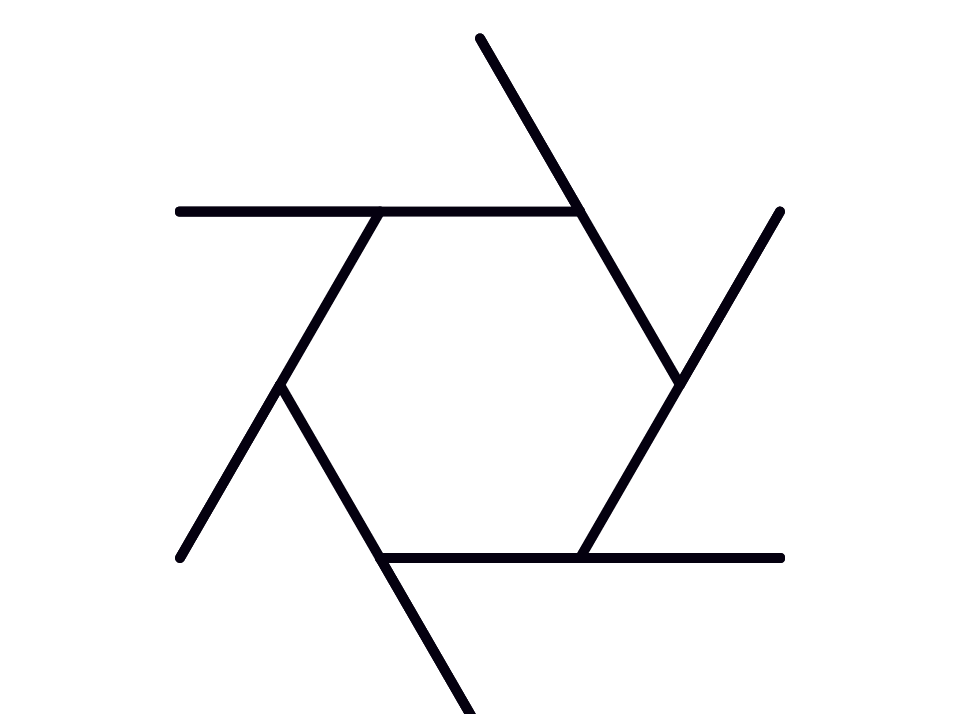
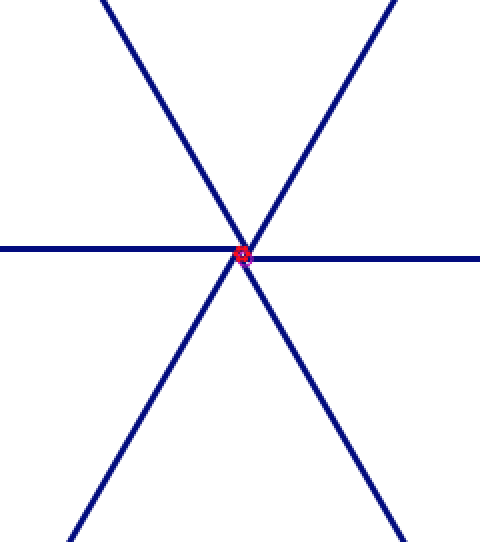
An easy way to do this is to notice that if you start from a corner and keep traveling along the polygon making a turn at each corner until you come back to where you started, you have made a full cycle of 360°. A bird’s-eye view of the tracks shown on the right, from high enough up that the racetrack looks like a single dot, might make this clearer.
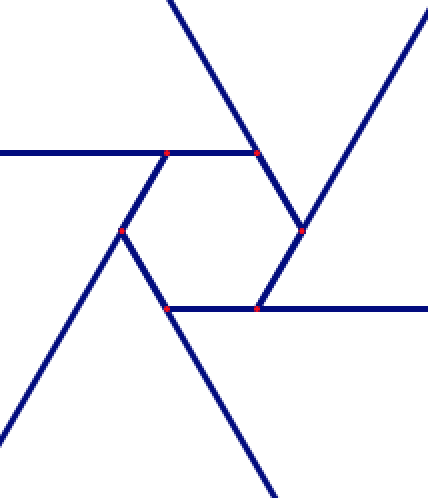
This animation may help:
![Shrinking polygon with turning angles Shrinking polygon with turning angles]()
Thus, the sum of all the turning angles must be 360°.
- What does this imply for each turning angle of
- An equilateral triangle?
- A square?
- A regular pentagon?
- A regular hexagon?
- A regular polygon with N sides?
- Test your answers and understanding on this interactive program.
- Now you know everything you need to create custom made Polygon block that will take the number of sides and side length as input and will draw the desired regular polygon.
Fill in all the blanks below. Build and test your code.