Flipping a Coin Project
AC:
- If I click on the the link in FYTD 1 and then hit escape (just trying it, looking for the code), things start disappearing.
- I really don't understand what FYTD 3 is asking. What is graphed against what here?
On this page, you will learn how to model the tossing of a coin.
![Flipping of a quarter Flipping of a quarter]()
When you toss a coin, you assume that the chances of getting a head or a tail are equal. But if you toss a coin 10 times, you know that you might not get exactly 5 heads and 5 tails. What percent of the time do you get that result? Is it different if you tossed the coin 100 times? 1000 times? It is tiresome and impractical to toss a coin hundreds or thousands of times, but it is possible to explore these questions with a simulation. In this project you will simulate the flipping of a coin and test your hypotheses.
-
Play with the Snap! file
linked here to see a possible implementation of what you are trying to achieve with your the simulation. Before starting to program in Snap!, plan out the sequence of events that will occur in your simulation:
- When and how will the user input the desired number of flips?
- How will the program simulate the coin toss mathematically?
- How will the program simulate the coin toss visually? What will the user see?
- What are the variables to create in order to keep track of the important parameters in the simulation? When should these be initialized? When should they be updated?
Before building your algorithm in Snap!, work through your pseudocode with a few example inputs until you have debugged it as much as possible.
Do this on your own but if you get stuck, you can visit
this page for hints.

Use this file to build a Snap! program to run the simulation. It includes a sprite named “Coin” with two costumes (Heads and Tails) and a sound file (“Pop”) to get you started in your work.-
If you toss a coin 10 times and repeat this 10-toss trial many times, how likely do you think each possible percentage of heads will be across all trials? Here are two examples of possible distributions of the percentage of heads across many 10-toss trials. Which shape of a histogram do you expect in your class simulations?
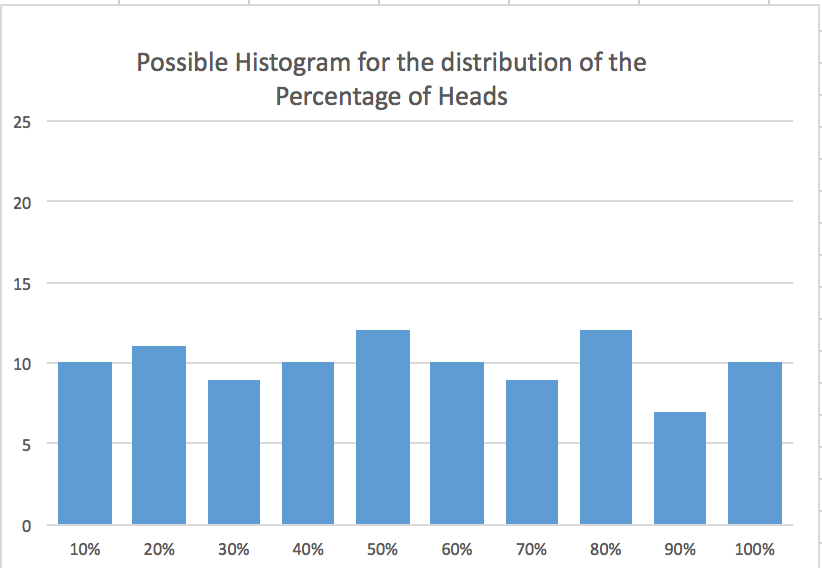
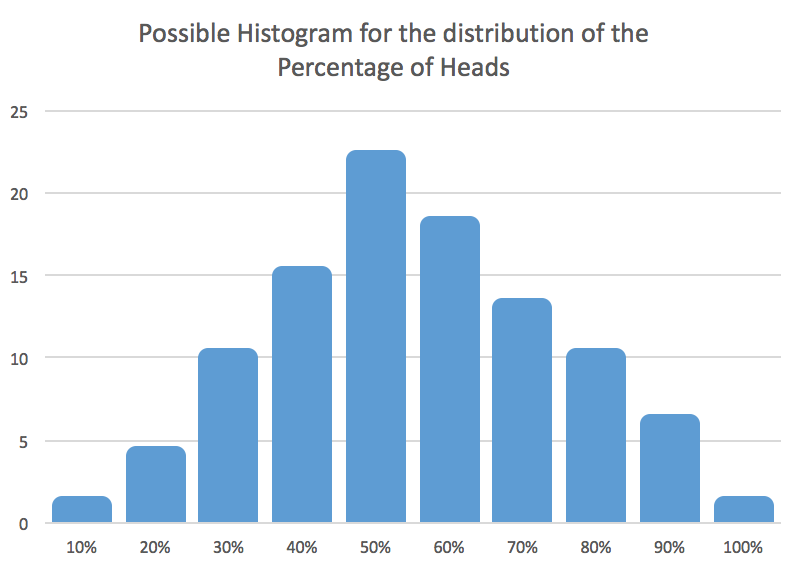
- Use your program to simulate tossing a coin 10 times and record the percentage of heads that is observed. Combine your results as a class to graphically display the distribution of this percentage with a histogram. Are the results in accordance with what you predicted?
- If you were to repeat the above experiment but this time tossing the coin 100 times (doing 100-toss trials), how would you expect your histogram of percentage of heads to change? Test your hypothesis using your simulation and combining the results as a class.
- Save a copy of your work and create code that simulates an unfair coin. For example, instead of the odds of heads vs. tails being 50:50, the respective likelihoods could be 75:25. Your program should ask the user to input what this bias should be.
-
On paper, study the mathematics behind tossing a coin a number of times. For example, in 3 tosses of a coin, what is the theoretical likelihood of getting:
Hint: you can do this most easily by first listing all the possible outcomes: HHH, HHT, etc.
- exactly 3 heads
- exactly 2 heads
- exactly 1 head
- no heads
- Create a Snap! program to simulate the rolling of a single die. Then extend your program to simulate the rolling of two dice. Create a variable to report the sum of the two dice. Predict which sum will occur most often if you rolled the dice 1000 times. Use your simulation to test your hypothesis.

