because .png "round (7.5)")
reports a value.On this page, you will consider a problem that can't have an answer.
By this point in the course, you've experienced the frustration of debugging a program. It would be great if there were a general-purpose debugging program that could read any code and determine if there were bugs. Unfortunately, we can use proof by contradiction (as Alphie, Betsy, and Gamal did on the previous page) to prove that this can't be done.
First, we'll assume that it's possible to write a function to determine if there are infinite loops in a program (situations in which a function runs forever without reporting a value). Then, we'll use that function in a program especially designed to create a contradiction (a logical incompatibility) to prove that the assumption is wrong—no general-purpose debugging program can exist. "Does this program have bugs" is an undecidable problem; no algorithm can ever be constructed that always solves it correctly for every program.
An infinite loop is a sequence of computer instructions that repeats forever.
An unsolvable problem is one for which no algorithm can ever be written to find the solution.
An undecidable problem is one for which no algorithm can ever be written that will always give a correct true/false decision for every input value. Undecidable problems are a subcategory of unsolvable problems that include only problems that should have a yes/no answer (such as: does my code have a bug?).
Halts? Function Exists
halts?; we are proving that it can't be written at all, no matter what code implements it.halts? that determines whether a given reporter will report a value in a finite time. (If so, we say that the reporter halts.) It takes two inputs: a function and an input value for that function. It reports true if the function would report a value when given that input; it reports false if the function would run forever (in an infinite loop).
For example, the function round will not run forever when given the input 7.5; it will report 8.
halts? code will treat the input function as data instead of running it. because reports a value.
On the other hand, imagine we had a function that will get stuck in an infinite loop when given the input foo; it would never report (never halt).
because .png "program with an infinite loop (foo)")
loops infinitely.
We'll use proof by contradiction to show that the following question can't be answered in general:
Will a certain computer program, given a certain input, report a result in a finite amount of time?
The "computer program" is the first input to halts?. The "given input" is the second input to halts?. And what halts? reports is either true or false: yes the "computer program" will halt or no it won't.
Note that halts? itself must always report a result, even if the program it's testing doesn't. This is because we are assuming (an assumption we'll show is false) that halts? always works—that it always reports an answer.
We can answer this question for some specific functions, but we are trying to determine whether we can devise a general test that will tell us whether any particular function will report a value for any specific input.
The "in general" part is important. Of course we can answer the question for certain particular programs. This one halts (reports a value) for any input:
This one never halts for any input:
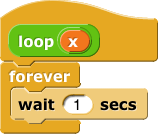
And this one halts sometimes—for any input except 87:
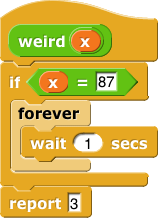
Recall: the question is whether we can devise a test that will tell us whether any particular function will report a value for any specific input.
halts? function does.halts? function in this proof by contradiction process.Halts? Won't Work
To prove there can be no such function, we need to create a contradiction. We need to show that there has to be at least one function and one input to that function for which halts? fails to work the way we assumed it does. So, we can make up a block, tester, specifically for the purpose of breaking halts?:
# and ⋮ symbols for inputs declared to be numbers or lists, the λ is not part of the input's name but is a type hint that was created when selecting the reporter input type:
tester will have a rounded gray ring to indicate that the input should be a reporter: .png "tester ()")
The forever block in this script creates an infinite loop. If the tester code ends up in this part of the if statement, it will never report anything. So whether tester itself will halt depends on the output of the halts? predicate in the if statement inside it.
The expression 
asks what will happen if we call the inputted function (reporter) with itself as its own input. This is similar to when Betsy made a statement about the statement she was making, when she said, "The statement I'm making right now is false."
This is challenging. Stick with it! We are creating a contradiction to prove that the halts? function called inside tester can't exist.
To make the situation exactly like what Betsy said ("The statement I'm making right now is false."), we'll call tester on itself:
Now, the if statement inside the tester block will ask if tester will halt (not run forever) if it's called with tester as its input. The predicate in the if statement will become halts? (tester) (tester).
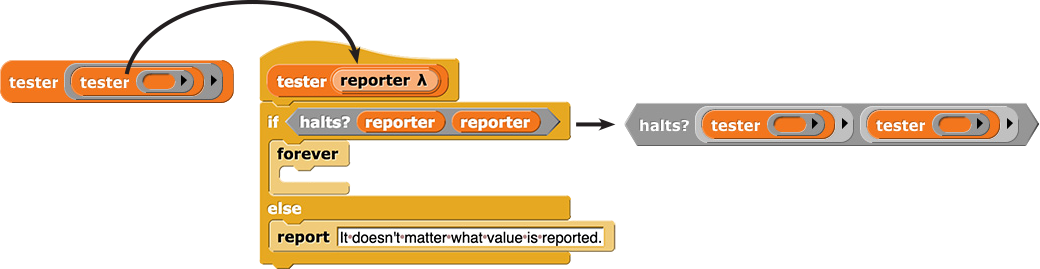
So, just as in the examples above,
would mean that returns a value.
would mean that loops infinitely.
When we call , we run into the contradiction. To see how, look back at the tester definition:
Showing that the result has to be wrong involves a case analysis like the ones used to solve the logic puzzles on page 1. Consider the two possible cases:
then tester will take the first branch of the if, and so it will loop forever. That means won't halt, and so halts? gave the wrong answer. then tester will take the else branch and report "It doesn't matter what value is reported." That means will halt, and so halts? is wrong again.tester reports, just that it reports some value, but it does matter what value halts? reports.No matter what halts? reports, it will always disagree with itself in a program like this. This contradiction (this logical impossibility) means that the assumption that it's possible write halts? has to be wrong. This isn't just a claim about what will happen in Snap!. The language you use to explore a computational problem can impact the clarity or readability of your code but not whether a solution to a problem exists. Even with advances in quantum computing, we will never be able to create a general-purpose debugging program. This famous example is known as the halting problem, and the fact that the halting problem is not decidable is the Halting Theorem.
Go over this whole proof again together. Make sure both you and your partner understand:
halts? does, and how halts? is going to be used in the prooftester function behaves (for any inputted function) leads to a contradictionAlan Turing (1912-1954) was one of the founders of computer science. He is known for two achievements. First, he made a massive contribution to winning World War II by inventing a mathematical theory and corresponding computer hardware to break the encoded messages generated by the German Enigma machine. Second, together with his colleague Alonzo Church, Turing was a founder of theoretical computer science: proving how computers must work regardless of future technology. Though his work on the Halting Problem, he proved that there are computations that can never be done, no matter how big and fast computers get.
When Turing did this work, there were no programmable computers; people had to rewire physical machines to solve each new problem. With powerful programming languages (such as Snap!), we can see and understand the essence of Turing's proof much more easily because we can use functions as inputs to other functions, as you've seen with map, keep, and combine. This proof was even harder for Turing because he had to invent the idea of a computer program that can itself be represented as data inside the computer.