We've looked at how the number of bits used to represent an integer affects how big it can be. Now we turn to the specific way a single-word integer is encoded as bits.
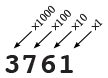
In base 10, there are ten digits (0-9), and each place is worth ten times as much as the place to its right.

In binary, base 2, there are only two digits (0 and 1), and each place is worth two times the place to its right.
In base 10 notation, each place value represents a power of ten: the units place (100 = 1), the tens place (101 = 10), the hundreds place (102 = 100), the thousands place (103 = 1000), etc. So, for example:
9827 = 9 × 103 + 8 × 102 + 2 × 101 + 7 × 100
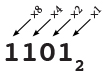
.jpg) Base 2 uses the same idea but with powers of two instead of powers of ten. Binary place values represent the units place (20 = 1), the twos place (21 = 2), the fours place (22 = 4), the eights place (23 = 8), the sixteens place (24 = 16), etc. So, for example:
Base 2 uses the same idea but with powers of two instead of powers of ten. Binary place values represent the units place (20 = 1), the twos place (21 = 2), the fours place (22 = 4), the eights place (23 = 8), the sixteens place (24 = 16), etc. So, for example:
100102 = 1 × 24 + 0 × 23 + 0 × 22 + 1 × 21 + 0 × 20 = 16 + 2 = 1810
To translate from binary (for example, 1011012) to base 10, first, write the number out on paper. Then write out the binary place values by doubling left from the units place:
| 1 | 0 | 1 | 1 | 0 | 1 |
|---|---|---|---|---|---|
| 32 | 16 | 8 | 4 | 2 | 1 |

|
|||||
This means that this number is, in base 10, 32 + 8 + 4 + 1 = 45. So, 1011012 = 4510.
To translate from base 10 (like 8910) to base 2, first write out the binary place values by doubling left from the units place until you get to a value larger than your number (128 for this example). Then think, "I can take out a 64, so I write a 1 there, and there's 25 left (89 − 64). I have 0 thirty-twos, because I only have 25. But I can take out 16, and there's 9 left. So, 8 and 1 are the last nonzero bits.
|
0 |

|
|||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | |
Now, read the number off: 10110012 = 8910.
Here's a more precise description of this algorithm to find the base 2 representation of any positive integer:
The string of ones and zeros you have recorded is the binary representation of your original number.
(Change from a "comment" to a "sidenote" when page is complete.) --MF, 11/20/17