Script Variable Projects

You could replace the below with one of these:
"U2L2-MathTools"Start a New Project called U2L2-MathTools
(sizing is only off because it's in a reviewer comment). --MF

Open a new file. Create a new project

You have a choice. Some of the problems below are about language or linguistics, some are about mathematics, and some are about art. Choose any three that interest you and do them.

  1. Mondrian—an art project: The Dutch artist Piet Mondrian is possibly best known for his artwork using brightly colored rectangles.

    Tableau_I,_by_Piet_Mondriaan, from Wikimedia Commons "Tableau 1" by Piet Mondrian

    Mondrian wasn't at all random in his choice of colors and locations, but even some random choices can be interesting. A snap script can produce designs like these.

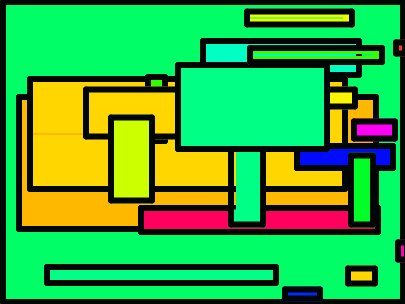
    Mondrian-like art drawn with Snap another Mondrian-like design drawn with Snap

    This isn't the actual Snap! program. You could write custom blocks with these names, but they're a little verbose to use as real block names, especially that two-line one in the middle. This algorithm is for you to read, not for a computer to read.
    This algorithm produced those designs:
    Draw outer frame (400 x 300); Fill with some color; Repeat many times; Pick random location, Pick random height and width for a rectangle that, at that location, won't extend beyond frame; Draw rectangle boundary in thick black line; Fill rectangle with random color

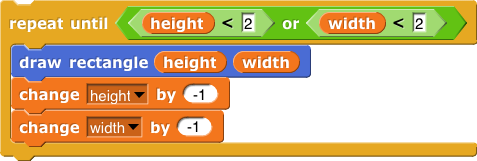
    To keep your code clear, you may want to create separate blocks that specialize in boundary and fill and choosing locations and calculating size.

    snap has no fill with color block. One way to make such a block is
    Repeat until height or width is less than 2; Draw rectangle of specified height and width; Set height slightly smaller; Set width slightly smaller

    To get bright colors, use set pen shade to 100, and you get a good collection of colors with set-pen-color-to(2-times-pick-random-0-to-50)

    1. Build a program that draws different pictures each time, always using colored rectangles. Use the algorithm suggested above or some idea of your own. Take screen shots of the artworks your program generates and save the ones that you like best.
    2. Mondrian limited his colors and used a lot of white and some black. Experiment with that to see if you get designs you like.
    3. Find ways to improve your program.
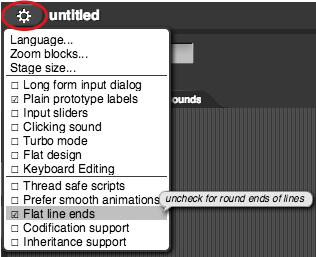
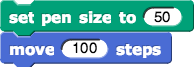  2. Another art idea: The code Set-pen-size-50-move-100-steps does not do what you might expect, because the "ends of the lines" are rounded. Try it. Now clear the stage and try Set-pen-size-50-move-0.1-steps.
    Why does that happen? Talk with Your Partner
    colored circles randomly placed colored ovals
    Experiment with the possibilities.
    You can choose between flat and round ends in the settings menu.
    settings menu, flat line ends
    If you switch to "Flat line ends" for this project, you will probably want to switch back to "round ends" for other drawing projects.
  3. Writing secret code: Create a block that takes a word as input, changes each letter into the next letter in the alphabet—for example, A becomes B, Y becomes Z...—and reports the result, like this: encode-decode(HANDY)-with-result(IBOEZ).

    In order to do this, you will need to be able to change a letter into a number, add 1 to that number, and then change the new number back to a letter. The blocks unicode-of(Y) and unicode(89)as-letter will help you do that. Experiment with them to see how they work.

    1. This block encodes by adding 1 to the unicode for each letter. You could, instead, always add 2 or 5 or whatever. Give your block a second variable that allows you to specify what to add to the unicode.
    2. When you give your encode block the input z, what does it report? If that's not what you would like it to report, change it.
    3. Make a decode block.
  4. Linguistic research: Build a block that can take a piece of text as input and which letter, t or s, is used more often in that bit of text. Later, you will be able to generalize this and take a large block of text and figure out the frequency of each letter. Letter frequency differs from language to language. That information has been used as one clue in decoding encrypted messages.
  5. A mathematical function: Create a factorial block n factorial (or n!) that takes a positive integer n and reports the product of all whole numbers from 1 through n, in other words 1 × 2 × 3 × ... × (n - 1) × n. When the input is 4, the output should be 24 (because 1 × 2 × 3 × 4 = 24).
    1. Dividing 5! by 4!, the result should be 5 5-factorial-divided-by-4-factorial-with-result(5) because 5 factorial is really just 5 times 4 factorial. Using your block, check each of these computations—4-factorial-divided-by-3-factorial, 3-factorial-divided-by-2-factorial, 2-factorial-divided-by-1-factorial and 1-factorial-divided-by-0-factorial—to see what it reports. One of these is inconsistent with the others. To fix the problem, we need to define 0! = 1. Edit your n! block to report 1 if n = 0. Then fully test n! again to make sure it works as it should.
    2. Debugging: Obviously cookie-factorial-bug should not work. Check to see what does happen. Then edit your block and find a way to use is n a number to check that the input is a number and report some sensible result or message.
    3. Analyzing code: In mathematics, factorial is defined only for positive integers and zero, so 3.7! would make no mathematical sense. But three-point-seven-factorial reports a result. Find out what it reports and analyze what the block does so that you can figure out why that is the result.
  6. Another mathematical function: Create a block triangular number n that adds all of the whole numbers from 1 through n:$$1 + 2 + 3 + \cdots + (n - 1) + n$$ When its input is 4, your block should report 10 (that is, 1 + 2 + 3 + 4). Define your block so that triangular number 0 reports 0.
    1. Create sum from a to b so that sum from 3 to 7 reports the sum 3 + 4 + 5 + 6 + 7, and sum from -3 to 3 reports the sum of -3 + -2 + -1 + 0 + 1 + 2 + 3.
  7. Recall that n mod i will tell you if i is a divisor of n.
    Counting divisors: Create a block that takes a whole number as input and checks numbers from 1 through that input and counts the ones that evenly divide the input. So, for example, number of divisors of 8, with result = 4 because, from 1 through 8, only the numbers 1, 2, 4, and 8 evenly divide 8. number-of-divisors 10 should also report 4 because, of the numbers from 1 through 10, only 1, 2, 5, and 10 are divisors of 10. Experiment to find several numbers that have an odd number of divisors.
 
  1. "Flat line ends" should be unchecked for this one.
    Here is a block and the picture it makes.

    Block that makes nested colored circles, looking a bit like a tunnel The picture of nested circles made by that block

    Edit it and give it inputs that let you produce pictures like these. You don't have to use script variables.

    command three embedded red circles

    command tunnel-(steps-4)(color-50) four embedded aqua-blue circles

    Experiment with various inputs.

  2. The artist Joseph Albers became famous for paintings a bit like this: AlbersPic-(steps-4)(color-60) Albers-(steps-4)(color-60)

    Set "flat line ends" and create a block that draws pictures like this. It will be convenient to use script variables

  3. Edit your raise (n) to the power (b) block to make it work for negative integer exponents.
  4. Old-fashioned divisibility test—divisibility by 3 or 9:
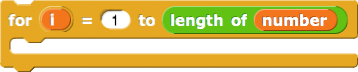
    • Create a helper reporter digit sum that adds up the digits in a number. So, for example digit sum 7 should report 7, and digit sum 12 should report 3, and digit sum 126 should report 9 (the sum of 1, 2 and 6). You may find these blocks useful. fletter-i-of-number for-i=1-to-length-of-number
    • Then write repeated digit sum, which keeps taking the digit sum until the result is a single digit. For example, the digit sum of 238 is 2+3+8=13, which is more than a single digit. The digit sum of 13 is 1+3=4, which is a single digit. So the repeated digit sum of 238 is 4.
    • Write predicates divisible by 3? and divisible by 9?. A number is divisible by 3 if its repeated digit sum is 0, 3, 6, or 9; it's divisible by 9 if its digit sum is 0 or 9.
      • Tough StuffTough Stuff Why?
  5. Old-fashioned divisibility test—divisibility by 7: Create a multiples of 7 algorithm block that takes any whole number as input and then puts it through this process:
    Again, the link starts a new project. But students can load the library themselves. Only projects meant to replace the previous work should be linked this way!
    For this project, all but last letter of and last letter of are useful. They are in the Words, sentences library.

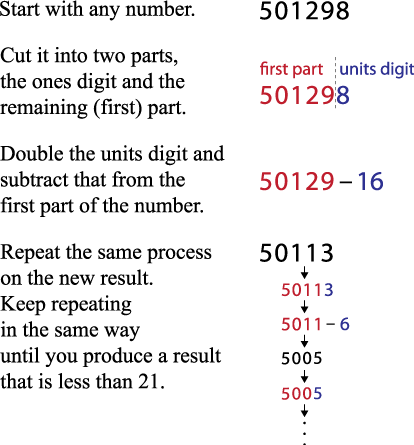
    multiples of 7 algorithm

    Test it first on several multiples of 7 (small and large) and make sure that, for multiples of 7, it reports only the results 14, 7, 0, -7, and -14. Also test it on several numbers that are not multiples of 7; for those numbers, it should never report 14, 7, 0, -7, or -14. multiples-of-7-algorithm-block-with-501298-as-input(and-result-neg14)

  6. Look up a test for divisibility by 11 or 13 and see if you can build a block that performs that algorithm.
    7. In snap, as in most programming languages, you can test for divisibility just by using mod, but before computers were widespread, algorithms like these greatly simplified some computations.
Import ToolsAlthough this set variable to function of variable style of programming is very common, pretty soon you'll learn a better way: functional programming, in which you never change the value of a variable. You're not quite ready to write functional programs yet (that'll come in Unit 3), but here are some examples from above, rewritten functionally, that you can probably understand:
factorial: combine with times items of numbers from 1 to nnumber-of-divisors: length of keep items such that ((n mod __) = 0) from (values from 1 to n) digit sum: combine with + items of word to list of number
"U2L2-MathTools"save your work as U2L2-MathTools