 that reports whether or not a set of numbers forms a magic square. In a magic square, the sum of the numbers in each row, column, and diagonal must be equal.
that reports whether or not a set of numbers forms a magic square. In a magic square, the sum of the numbers in each row, column, and diagonal must be equal.In this lab, you will write  that reports whether or not a set of numbers forms a magic square. In a magic square, the sum of the numbers in each row, column, and diagonal must be equal.
that reports whether or not a set of numbers forms a magic square. In a magic square, the sum of the numbers in each row, column, and diagonal must be equal.
The data in this list:  corresponds to this 3-by-3 grid of numbers:
corresponds to this 3-by-3 grid of numbers:
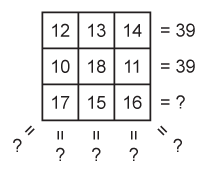
is a magic square? should report true or false.




Now that you've had some experience deciding what makes something a magic square, it's time to write an algorithm.

One of the things that will be useful when you write is _ a magic square? is a reporter that picks off elements from a given list, like the first, fourth, and seventh element.
 . Here's how it starts:
. Here's how it starts:
And here it is in action:
