, which will allow you to sort a list. Sorting the list will take a decently long time, so we'll want to do it as few times as possible. How many times will you need to sort the list for each test run?
Unsorted data doesn't give you a lot to work with. Your knowledge is limited to strictly the most obvious information: the numbers themselves. This makes strategy somewhat non-existent; the best you can do, on average, is to simply start at the beginning and search through the list one by one. This approach can become incredibly slow if we're dealing with a lot of data, but is actually fairly quick when working with smaller amounts of data. In addition, the block is relatively straightforward to create and doesn't require the data to be put into a particular order to work. The block should return the location of the number in the list, or zero if the number doesn't exist in the list.
You could say that putting information in a particular order (lowest to highest, for example) actually creates new information. Instead of being a simple list of numbers, sorting the information adds order and allows us to make additional assumptions that we weren't able to make before. This type of information is different from the numbers themselves: it is not stored in a variable or list, but becomes a property of the information itself. We can use the property to reduce the number of checks we have to do to find a particular number. The trade-off to this, however, is that we need to sort the list (which takes time) before we can make use of the order.
The provided framework includes , which will allow you to sort a list. Sorting the list will take a decently long time, so we'll want to do it as few times as possible. How many times will you need to sort the list for each test run?
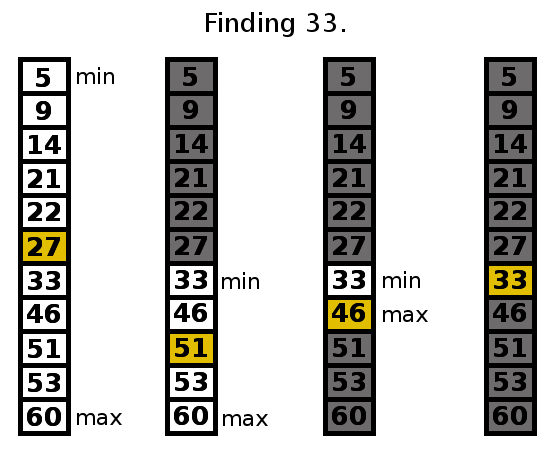
Searching through sorted data, while faster, also requires a more complicated block. We won't need to search through every space in the list anymore -- we can assume that many of them won't work. We can keep track of the range of numbers in a list that are a possible solution to the problem (see diagram) by recording the minimum and maximum slots that could possibly contain our number. This range should shrink after each guess because you can throw away the half of the numbers on the wrong side of the center point. Here's how things should generally work:
Let's say this application is going to be used to find many numbers every time it is launched -- possibly the same number multiple times. How could we speed this process up even more?