Trees in a Forest

Anatomy of a Recursive Block

For our tree block, we're going to point out various parts of the anatomy of a recursive procedure. The line numbers mentioned below refer to the picture at the right.

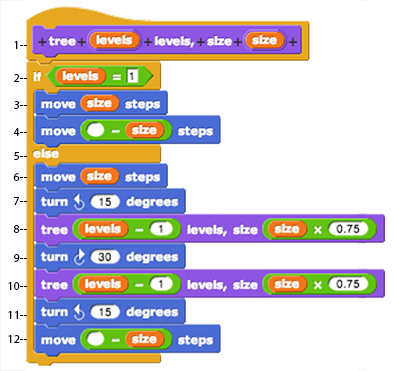
We always need a way to figure out that we're done and shouldn't call the recursive call again. Lines 2-4 are the Base Case, in which we handle a situation so simple that we don't need to call the block recursively.

If this isn't the base case we think to ourselves "Whoa — That seems complicated. I'll just do a small part of the problem and delegate to someone else". Here's what we do:

draw the trunk of the tree (line 6),
position the sprite for the left sub-tree (line 7),
delegate to another call to the tree block the drawing of the left sub-tree (line 8),
re-position the sprite for the right sub-tree (line 9),
delegate to another call to the tree block the drawing of the right sub-tree (line 10),
re-position the sprite to retrace the trunk (line 11), and
retrace the trunk and leave the sprite exactly where it started out (line 12).

Lines 6-12 are the Recursive Case, in which the block calls itself using recursion.

The Recursive Case also has to work towards the base case. This means that some input or other aspect of the recursive calls in the Recursive Case has to be changing such that the Base Case is eventually called. For our tree block, we are subtracting 1 from the level input of each recursive call, so that eventually the level input will reach a value of 1, which is the condition for our Base Case. If we cannot reach our Base Case, our block will keep recursively calling itself forever, getting stuck in what we call an infinite loop. This is what happened with our tree block before we modified it.

What would happen if we ran our tree block with a level input of less than 1? Think about it before you try it out.
Sometimes you can make a recursive procedure more elegant by having a smaller base case. In our tree program, what would a "zero level" tree mean? Try rewriting tree so that the base case is level=0.
See if you can make a tree like the first picture in this activity:

It is different from what we have done so far because the smaller trees are drawn part way up the trunk, instead of at the top of the trunk, and because the pen color is green for the lowest-level branches (the tree1-like ones) and brown for the others. You do not have to get it exactly like the picture; just try to make a more realistic-looking tree.