Recursive Tree, Part 1
- JK: Teachers at the EDC PD day (and I saw this in NY too) were confused by the name of the block. I think this is partly because it's called
tree1 in the text, but really should be called tree1 size. The fact that "size" appears twice confuses lots of people. (I think getting rid of the plus signs in the image will be helpful too.)
Our goal is to draw a tree like this.

We'll start with a simpler version that shows the technique clearly, although less prettily:
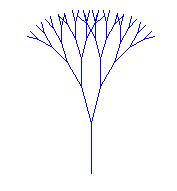
Technically, all the images in this unit are just approximations to fractals, because the smaller pictures are simpler than the complete picture. You have to imagine that we have infinitely many smaller and smaller branches.
The key to understanding this technique is to see that the tree is a fractal, that is, a picture that contains smaller versions of itself:

We're going to create a tree block in Snap!. It'll start with a move block to draw the trunk of the tree, then a turn block turning left, then a tree block to draw the left smaller tree, and so on.
"Wait!" you're probably thinking. "How can we use a tree block inside a tree block? It doesn't exist yet!" That's the big idea for this assignment.
We're going to work up to the complicated tree starting with very simple steps that don't involve tree-within-tree.
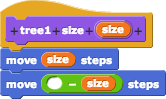
- Make a
tree1 block (so named because it draws just one level of the tree) using this script:
The empty input in the - block doesn't get anything put in it from a list; we aren't using higher order functions here. This just says to move -size steps.
This looks ridiculously simple, but trust us, it'll get interesting soon. When run, the script draws one tree branch, and then moves the sprite back
to its original position. That's going to be really important when we start using scripts within scripts; we always want to be able to assume that our
tree blocks leave the sprite in the same position and direction as it started in.
- Point the sprite facing upward, and put the pen down. Then try
tree1 size 50. You should get a result something like this:
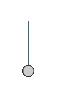
- Make a
tree2 block that draws two levels. Actually, you're going to make two different versions of this, so call the first one tree2a.
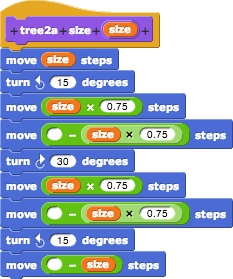
When run, it should give this result:

At this rate you'll never be able to make the beautiful version of the
tree in this century. In the next step, we'll discuss how to simplify
this process.
Before going on, make sure that you can
mentally trace through the code provided. Paying close attention to the
move and turn blocks is going to be important to see the big picture and
understand the recursion.
How many blocks would you need to write tree3a out of Motion blocks similarly to how we wrote tree2a? How about tree4a?






