
Using recursion we can make beautiful things! In this exercise you will learn to make the Koch snowflake (below).

The entire snowflake consists of three copies of a fractal, arranged in a triangular shape:
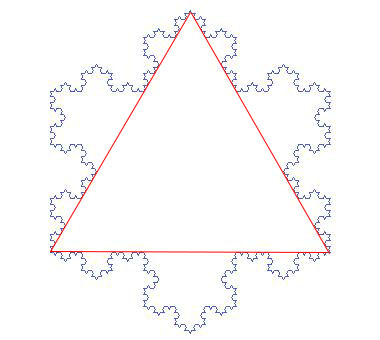
Unlike the tree and the earlier triangle fractals, this one does not return to the same place after each recursive call.
For example, the base case has the sprite start on the left and go to
the right (below).

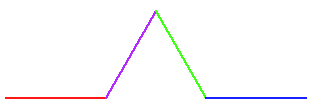
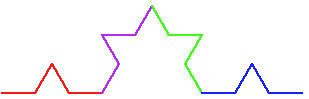
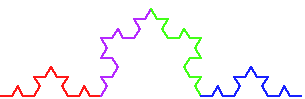

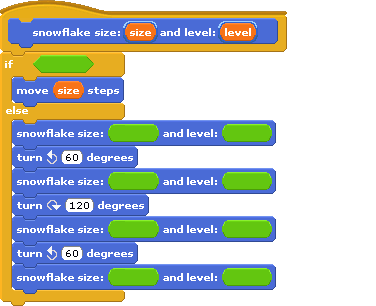
size in each recursive call have to be one third of the caller's size? There are four copies; why not one fourth size? Why exactly one third?
These pictures are clearly related to, but not quite the same as, the Koch curve. See if you can generate pictures like these.