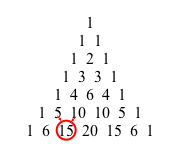
Perhaps you remember this picture from a high school mathematics class:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
︙
This is Pascal's Triangle.
Each number in the triangle is the sum of the two numbers above it:

In this example, 15 = 5+10. The numbers at the ends of each row, which don't have two numbers above them, are always 1.
We're going to want to refer to positions within the triangle by row and column numbers, so it may be easier to think about these positions if you align the columns this way:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
The rows and columns are numbered starting from 0, not 1, so the picture shows rows 0‒6. That way, the numbers in column 1 are equal to their row number. So, for example, the number in row 6 column 3 is 20.
Your mission is to write a pascal block that takes two numbers, row and column, as inputs. It should report the value at the corresponding position in Pascal's Triangle.
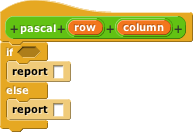
If you prefer to solve puzzles without hints, finish the definition now. Otherwise, turn the page.
The triangle is named (among Europeans and their cultural descendents) after the mathematician Blaise Pascal, who published a detailed study of the triangle in 1653, although the earliest surviving reference to the triangle comes from the Hindu mathematician Pingala, who lived some time around the 4th to 2nd century BCE.
The numbers in Pascal's triangle turn up in several different mathematical contexts. For example, numbers from Pascal's Triangle tell you how many ways you can choose column items from a set of row items. So, if you want to choose two people from Adele, Brian, Cindy, David, Evelyn, and Frank, there are 15 (row 6, column 2) ways to do it: Adele and Brian, Adele and Cindy, ... Evelyn and Frank.