PG: I'm glad this now has references to the extensions (and is no longer called Astrid). I like the idea of turtlifying it, though only the hint directs students away from a turtle solution. Using the method of locating the points by algorithm, storing them, then using that list of coordinates will be simpler than pure turtle, possibly even for the cardioid and other such envelopes inside a circle). I'd be inclined to have it start with just the animated image, and another one, a bit slower, animating the cardioid development in a circle (one end moves a step at a time, the other end two steps for cardioid), letting kids figure out what generating rule is involved. It's just personal taste, but I find "With your partner discuss" to be such a lame schoolish Micky Mouse instruction—no real setting tells us to discuss with our partner. And what business, in an optional project do we have saying "develop an algorithm and then use abstraction"? What sense does it make for us to say how to do what students don't have to do at all? With the slowly developing image (the current animation is just fine) students should have enough information to invent, if they like.
BH: See the red boxes.
MF: Needs rewrites
Este diseño utiliza líneas rectas para hacer formas que se ven curvas y a veces se cose con hilo o se dibuja en papel. Aquí hay algunos ejemplos y variaciones de este diseño hecho con cuerdas, computadoras, lápices sobre papel e incluso lápices pegados entre sí:
A continuación se muestra una tabla parcial de coordenadas para el primer cuadrante del diseño, que muestra qué puntos del eje y están unidos a qué puntos del eje x.
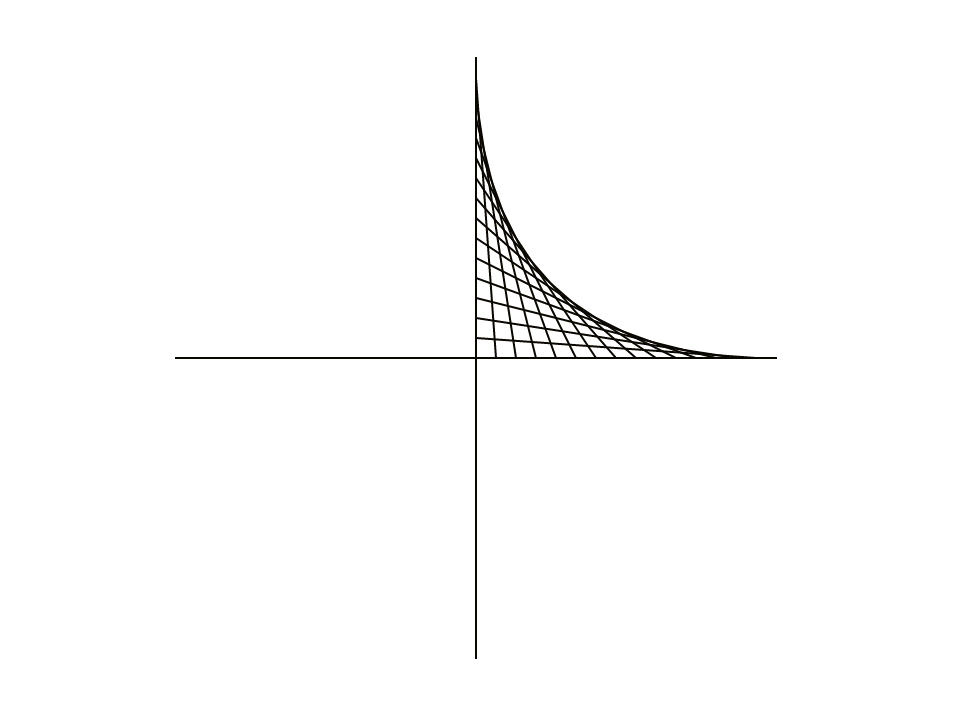
| Desde (eje y) | Hasta (eje x) |
|---|---|
| (0, 150) | (0, 0) |
| (0, 140) | (10, 0) |
| (0, 130) | (20, 0) |
| ... | ... |
| (0, 20) | (130, 0) |
| (0, 10) | (140, 0) |
| (0, 0) | (150, 0) |
Haz clic para una sugerencia sobre cómo comenzar este programa en Snap!
para:

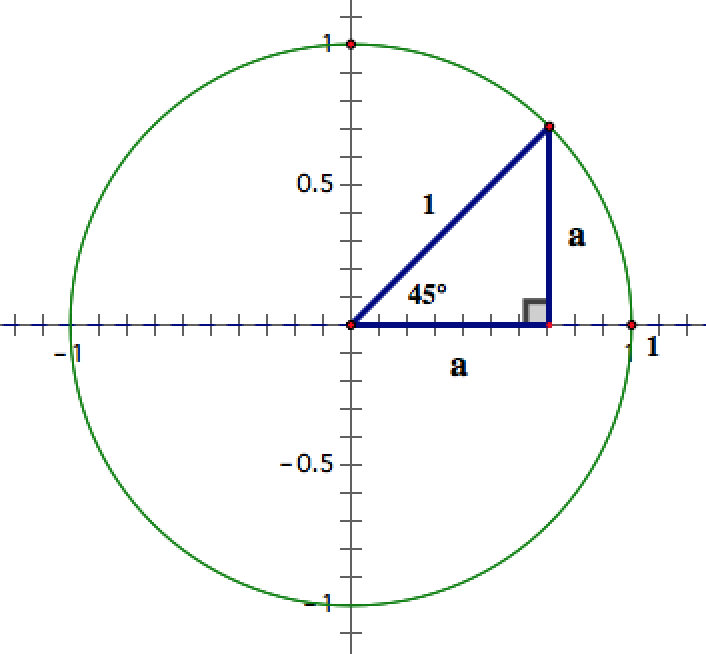
Podrías usar el teorema de Pitágoras:
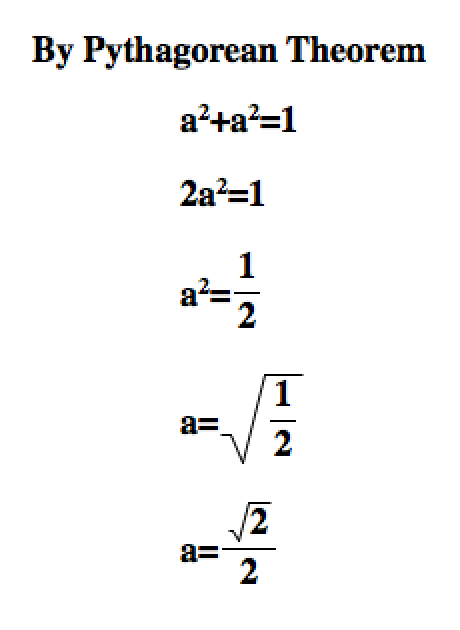



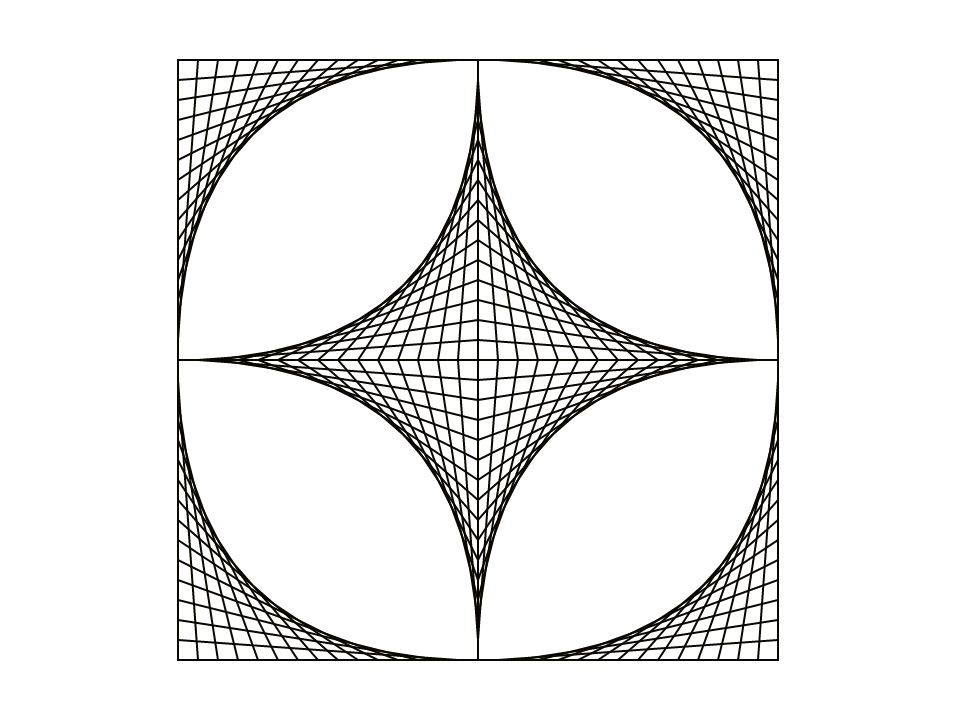
Esta animación explora el concepto artístico de "espacio negativo" mediante el uso de una cuadrícula de copias giratorias del diseño. ¿Cómo revisarías tu programa para generar animaciones como esta?
