Hemos visto cómo el número de bits utilizados para representar un entero afecta lo grande que puede ser. Ahora pasamos a la forma específica en que un entero de una sola palabra se codifica como bits.
La palabra "bit" es una abreviatura de la expresión en inglés binary digit (dígito binario).
Las personas generalmente usan dígitos de base diez (decimales) para escribir números. Las computadoras usan la base dos (binaria).
Ena notación de base 10, hay diez dígitos (0-9), y cada lugar vale diez veces el lugar a su derecha.

En binario, base 2, solo hay dos dígitos (0 y 1), y cada lugar vale la pena dos veces el lugar a su derecha.
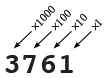
En notación de base 10, cada valor de lugar representa una potencia de diez: el lugar de las unidades (100 = 1), el lugar de las decenas (101 = 10), el lugar de las centenas(102 = 100), el lugar de las unidades de mil (103 = 1000), etc. Así, por ejemplo,:
9827 = 9 × 103 + 8 × 102 + 2 × 101 + 7 × 100
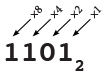
.jpg) Base 2 utiliza la misma idea pero con potencias de dos en lugar de potencias de diez. Los valores de lugar binario representan el lugar de las unidades (20 = 1), el lugar de los dos (21 = 2), el lugar de los cuatro (22 = 4), el octavo lugar (23 = 8), el lugar de los dieciséis (24 = 16), etc. Así, por ejemplo:
Base 2 utiliza la misma idea pero con potencias de dos en lugar de potencias de diez. Los valores de lugar binario representan el lugar de las unidades (20 = 1), el lugar de los dos (21 = 2), el lugar de los cuatro (22 = 4), el octavo lugar (23 = 8), el lugar de los dieciséis (24 = 16), etc. Así, por ejemplo:
100102 = 1 × 24 + 0 × 23 + 0 × 22 + 1 × 21 + 0 × 20 = 16 + 2 = 1810
Para traducir desde binario (por ejemplo), 1011012 a base 10, primero, escribe el número en un papel. A continuación, escribe los valores de lugar binario duplicando la izquierda desde el lugar de las unidades:
| 1 | 0 | 1 | 1 | 0 | 1 |
|---|---|---|---|---|---|
| 32 | 16 | 8 | 4 | 2 | 1 |

|
|||||
Esto significa que este número es, en base 10, 32 + 8 + 4 + 1 = 45. Entonces, 1011012 = 4510.
Para traducir desde la base 10 (como 8910) a base 2, primero escribe los valores de lugar binario duplicando a la izquierda desde el lugar de las unidades hasta llegar a un valor mayor que su número (128 para este ejemplo). Entonces piensa, "Puedo sacar un 64, así que escribo un 1 allí, y quedan 25 (89 − 64). Tengo 0 treinta y dos, porque solo tengo 25. Pero puedo sacar 16, y quedan 9. Entonces, 8 y 1 son los últimos bits distintos de cero.
|
0 |

|
|||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | |
Ahora, lea el número desactivado: 10110012 = 8910.
Aquí hay una descripción más precisa de este algoritmo para encontrar la representación binaria de cualquier número entero positivo:
La cadena de unos y ceros que has registrado es la representación binaria de tu número original.