Binary Representation
We've looked at how the number of bits used to represent an integer affects how big it can be. Now we turn to the specific way a single-word integer is encoded as bits.
:
Bit
DAT-1.A.3
The word "bit" is an abbreviation for binary digit.
DAT-1.C.1
People generally use base ten (decimal) digits to write numbers. Computers use base two (binary).
DAT-1.C.3
In base 10, there are ten digits (0-9), and each place is worth ten times as much as the place to its right.
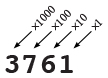
DAT-1.C.2
In binary, base 2, there are only two digits (0 and 1), and each place is worth two times the place to its right.
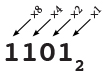
The subscript 2 on 11012 means the 1101 is in base 2. Numbers are normally written in base 10, so a subscript 10 is only used when needed for clarity.
Reading Binary
DAT-1.C.5
In base 10 notation, each place value represents a power of ten: the units place (100 = 1), the tens place (101 = 10), the hundreds place (102 = 100), the thousands place (103 = 1000), etc. So, for example:
9827 = 9 × 103 + 8 × 102 + 2 × 101 + 7 × 100
DAT-1.C.4
.jpg) Base 2 uses the same idea but with powers of two instead of powers of ten. Binary place values represent the units place (20 = 1), the twos place (21 = 2), the fours place (22 = 4), the eights place (23 = 8), the sixteens place (24 = 16), etc. So, for example:
Base 2 uses the same idea but with powers of two instead of powers of ten. Binary place values represent the units place (20 = 1), the twos place (21 = 2), the fours place (22 = 4), the eights place (23 = 8), the sixteens place (24 = 16), etc. So, for example:
100102 = 1 × 24 + 0 × 23 + 0 × 22 + 1 × 21 + 0 × 20 = 16 + 2 = 1810
To translate from binary (for example, 1011012) to base 10, first, write the number out on paper. Then write out the binary place values by doubling left from the units place:
1011012 has only six digits, so we don't need powers of two to the left of that.
| 1 |
0 |
1 |
1 |
0 |
1 |
| 32 |
16 |
8 |
4 |
2 |
1 |

|
This means that this number is, in base 10, 32 + 8 + 4 + 1 = 45. So, 1011012 = 4510.
DAT-1.C part a
-
Translate these binary representations into base 10 notation:
- 1012
- 1112
- 10100112
- 10000000002
Writing Binary
To translate from base 10 (like 8910) to base 2, first write out the binary place values by doubling left from the units place until you get to a value larger than your number (128 for this example). Then think, "I can take out a 64, so I write a 1 there, and there's 25 left (89 − 64). I have 0 thirty-twos, because I only have 25. But I can take out 16, and there's 9 left. So, 8 and 1 are the last nonzero bits.
Mary, this is a sloppy use of tables when I probably should be using some kind of CSS. Fix later. --MF, 12/8/17 There is a commented out, incorrect sidenote here. -bh

|
| 128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
| |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
I'm confused about why the arrow is going from right to left. Will that confuse students? Most of the work happens going left to right. Maybe there should be another arrow below the table that goes the other way... --MF, 2/12/18 It may be left over from when we were using the correct algorithm, which does go right to left. -bh
Now, read the number off: 10110012 = 8910.
Here's a more precise description of this algorithm to find the base 2 representation of any positive integer:
- First, find the largest power of two that is less than the number.
- Then, subtract that power of 2 from the number, keep the new number, and record a 1 in the place for that power of 2.
-
Then, determine if the next largest power of 2 that is less than the new number, and:
- If it does, subtract that power of 2 from the number, keep the new number, and record a 1 in the place for that power of 2.
- If it doesn't, keep the same number, and record a 0 for that power of 2.
Repeat this whole step with the next largest power of 2 until you have a bit (1 or 0) for all the remaining places down to and including the ones place (by which point you should have nothing left of the original number).
The string of ones and zeros you have recorded is the binary representation of your original number.
DAT-1.C part a
-
Represent these base 10 numerals in binary (base 2):
- 63
- 64
- 65
- 129
- 128
- 127
-
DAT-1.C part b
Put these numbers in ascending order without converting them to decimal notation:
- 10110012
- 110012
- 1000012
- 1010112
 What was your algorithm for comparing these numbers?
What was your algorithm for comparing these numbers?-
This question is similar to those you will see on the AP CSP exam.
A particular program uses 4 bits to represent whole numbers. When that program adds the numbers 9 and 7, the result is given as 0. Identify the best explanation of the result.
Data was corrupted during the operation due to a technical glitch.
While data corruption is possible, it is not a likely explanation for the recurrence of the result as one can demonstrate with repeated attempts to add 9 and 7.
The result was due to a round-off error.
There is no rounding done here.
The result was due to an overflow error.
Correct. 9+7=16, which is beyond the capacity of 4 bits to express. 0=(0000)2 is the first and 15=(1111)2 is the last integer expressible in a 4-bit system. 16=(10000)2 leads to an overflow.
A floating-point representation was used to approximate the result.
0 is not an approximation of 16.



.jpg) Base 2 uses the same idea but with powers of two instead of powers of ten. Binary place values represent the units place (20 = 1), the twos place (21 = 2), the fours place (22 = 4), the eights place (23 = 8), the sixteens place (24 = 16), etc. So, for example:
Base 2 uses the same idea but with powers of two instead of powers of ten. Binary place values represent the units place (20 = 1), the twos place (21 = 2), the fours place (22 = 4), the eights place (23 = 8), the sixteens place (24 = 16), etc. So, for example:

