-
 Watch this Hexadecimal and Binary Timer Snap! program run. The top row counts in binary, the middle in decimal, the bottom in hex. Write a description of the hex counter's behavior.
Watch this Hexadecimal and Binary Timer Snap! program run. The top row counts in binary, the middle in decimal, the bottom in hex. Write a description of the hex counter's behavior.
BH: SCRAP.
Typing long strings of ones and zeros is inconvenient and prone to error. A more efficient method is to use hexadecimal (base 16). One hex digit represents any whole number between 0 an 15. So eight digits of binary can be translated into two digits of hexadecimal, which is much easier and much less error-prone for humans.
| Eight bits in base two... | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | ||||
| 128s place | 64s place | 32s place | 16s place | eights place | fours place | twos place | ones place | ||||
| ...is two digits in base 16. | |||||||||||
| 161 | 160 | ||||||||||
| sixteens place | ones place | ||||||||||
| For example: 12110 = 011110012 = 7916 | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 7 | 9 | ||||||
| 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|
| A | B | C | D | E | F |
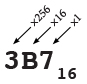
This stands for 3 \times 256 + 11\times 16 +7\times 1 or 951.
Base 16 uses powers of sixteen instead of powers of two or ten. Place values in hexadecimal represent the units place (160 = 1), the sixteens place (161 = 16), the two hundred fifty-sixes place (162 = 256), the four thousand ninety-sixes place (163 = 4096), etc. So, for example:
3B16 = 3 × 161 + 11 × 160 = 48 + 11 = 5910
To translate from hexadecimal (for example, 7B316) to base 10, first, write the digits on paper. Then write out the hexadecimal place values: start at the right with 1, then write 16 in the next place to the left, then write 256 (which is 162), and so on. Each new place will be worth 16 times the one to its right.
| 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|
| A | B | C | D | E | F |
| 7 | B | 3 |
|---|---|---|
| 256 | 16 | 1 |

|
||
So, 7B316 = (7 × 256) + (11 × 16) + (3 × 1) = 1792 + 176 + 3 = 197110.
To translate from base 10 (for example, 29910) to base 16, first write out the hexadecimal place values by multiplying by 16 moving left from the units place until you get to a value larger than your number (4096 for this example). Then think, "My number is smaller than 4096, so I leave that place blank. But I can subtract two hundred fifty-six once, so I write a 1 there, and there's 43 left. Now, I can subtract two sixteens, and there's 11 left. And 11 is B in hex."
| 0 |

|
|||
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 1 | 2 | B | |
Now, read the number off: 12B16 = 29910.
Notice that the algorithms for converting between binary and decimal are the same as the algorithms for converting between hexadecimal and decimal. These algorithms can be used to convert to and from any base.