Categorizar algoritmos

En esta página, compararás cuatro algoritmos y aprenderás cómo cada uno de ellos toma una categoría diferente de tiempo para ejecutarse.
  1. Localiza el bloque 25,000 enteros empezando desde () incluido en tu proyecto, y registra el tiempo que demora para varios números iniciales.
    Número inicial  Tiempo de 25,000 números enteros
    1000
    10,000
    100,000
    1,000,000
    10,000,000
  2. Habla con tu compañeroMira la tabla. ¿Cómo describirías lo que sucede con el tiempo a medida que el número inicial se hace más grande? Escribe una hipótesis sobre este patrón.
  3. Hay varias maneras diferentes de ordenar una lista, algunas de las cuales aprenderás en la Unidad 8. El bloque categoría utiliza un algoritmo de "categoría de inserción".
    Localiza el bloque ordenar 'ranura de entrada de lista' incluido en tu proyecto, y prográmalo para cada longitud de lista.
    Longitud de la lista Tiempo de la categoría
    10
    100
    1000
  4. Habla con tu compañero¿Cómo describirías lo que sucede con el tiempo a medida que el tamaño de la lista de entrada se hace más grande? Escribe una hipótesis.

Puedes clasificar los algoritmos por la cantidad de tiempo que tardan en ejecutarse.

: Tiempo lineal, tiempo sublineal, tiempo constante y tiempo cuadrático
  1. Vuelve a mirar tu tabla para la búsqueda lineal. Confirma que al multiplicar la longitud de la lista por diez, se multiplica aproximadamente el tiempo empleado por diez (tiempo lineal).
  2. Vuelve a mirar tu tabla para la búsqueda binaria. Confirma que el tiempo de búsqueda para cada lista de palabras es menor que para la búsqueda lineal (tiempo sublineal).
  3. Vuelve a ver tu tabla para los 25,000 números enteros. Confirma que toma aproximadamente la misma cantidad de tiempo independientemente de la entrada (tiempo constante).
  4. Vuelve a ver tu tabla para ordenar. Confirma que al multiplicar la longitud de la lista por diez, se multiplica aproximadamente el tiempo por cien. (tiempo cuadrático).

La diferencia entre la búsqueda lineal y la búsqueda binaria puede ser muy importante si se busca en una lista de diez millones de elementos, pero la diferencia más importante en el algoritmo de eficiencia está entre el tiempo polinómico (proporcional a cualquier potencia del tamaño de la entrada) y el tiempo exponencial.

: Tiempo polinómico y tiempo exponencial

En un algoritmo de tiempo exponencial, solo añadiendo 1 al tamaño de la entrada (n) of a 2n el algoritmo de tiempo ¡duplica el número de pasos! Así que, por ejemplo, si el tamaño de la entrada es 20, cualquier algoritmo de tiempo polinómico será lo suficientemente rápido, pero un algoritmo de tiempo exponencial puede tomar muchos años en finalizar.


AAP-2.M.2 text before bullets

Una razón por la que vale la pena aprender estas categorías es para evitar reinventar la rueda. Por ejemplo, has aprendido que si una lista está ordenada, puedes buscarla en tiempo sublineal utilizando la búsqueda binaria. Por lo tanto, cuando escribas un programa que necesite buscar en una lista repetidamente, vale la pena ordenar la lista antes de buscar. Conocer los algoritmos que ya existen puede ayudarte a construir nuevos algoritmos.

Todos los algoritmos que has explorado hasta ahora en este laboratorio (búsqueda lineal; búsqueda binaria; 25,000 números enteros; y ordenar) son algoritmos de tiempo razonable. La siguiente actividad opcional es un ejemplo de un algoritmo de tiempo exponencial.

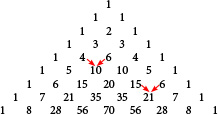
    Un problema que puede ser familiar y que requiere un algoritmo de tiempo exponencial es el de calcular cualquier elemento dado del Triángulo de Pascal. En el triángulo de Pascal, cada número se encuentra sumando los dos números de arriba. Por ejemplo, 4 + 6 = 10 y 15 + 6 = 21 como se muestra abajo. El primer y último número de cada fila, que no tienen dos números encima de ellos son 1.
    1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 triángulo de Pascal, fila: (6) posición (3) reporta 10

  1. Localiza el bloque triángulo de Pascal, fila: () posición: () incluido en tu proyecto, y prográmalo para varias entradas.
    Si tardan demasiado en ejecutarse, puedes detener el programa; solo tienes que rellenar la tabla hasta donde te permita la velocidad de tu computadora.
    Entradas Triángulo de tiemo de Pascal
    5, 2
    10, 5
    15, 7
    20, 10
    25, 12
    El valor de la  fila es la entrada del triángulo de Pascal que interesa. (La entrada de posición solo se da para obtener un tiempo para una de las posiciones cercanas al centro de la fila, que tardan más en calcularse.)

    Estas entradas de fila son muy pequeñas comparadas con el tamaño de la entrada de los algoritmos de búsqueda lineal, búsqueda binaria, y ordenar, y aún así el tiempo requerido para el triángulo de Pascal es mucho mayor. Tu computadora probablemente no puede hacer mucho más allá de los 25.

    Este algoritmo funciona sumando los dos números de arriba usando el algoritmo dentro de sí mismo recursivamente, pero hay mejores algoritmos que calculan el valor de un número en el triángulo de Pascal en tiempo lineal.
    AAP-4.A part a
  1. Escribe un párrafo que explique la diferencia entre los algoritmos que se ejecutan en un tiempo razonable y los que no lo hacen.
  2. Esta pregunta es similar a las que verás en el examen de AP CSP.
    La siguiente tabla muestra el tiempo que tarda la computadora en realizar varias tareas sobre los datos de ciudades de diferentes tamaños.
    Tarea Ciudad pequeña
    (población 1,000)    		 Ciudad mediana
    (población 10,000)    		 Ciudad grande
    (población 100,000)
    Entrada de datos 2 horas 20 horas 200 horas
    Copia de seguridad de los datos 0.5 hora 5 horas 50 horas
    Búsqueda a través de los datos 5 horas 15 horas 25 horas
    Clasificación de datos 0.01 hora 1 hora 100 hora
    Basado en la información de la tabla, cuál de las siguientes tareas es probable que tome la mayor cantidad de tiempo cuando se amplía para una ciudad con una población de 1,000,000.
    Entrar datos
    Realizar una copia de seguridad de los datos
    Buscar entre los datos
    Clasificar datos