Categorizing Algorithms

TG and solutions need to be checked. --MF, 12/19/18

On this page, you will compare four algorithms and learn how they each take a different category of time to run.
  1. Locate the 25,000 integers starting from () block included in your project, and time it for various starting numbers.
    Starting Number 25,000 integers Time
    1000
    10,000
    100,000
    1,000,000
    10,000,000
  2. Talk with Your Partner Look at the table. How would you describe what happens to the time as the starting number gets bigger? Write a hypothesis about the pattern.
  3. There are several different ways to sort a list, some of which you will learn about in Unit 8. This sort block uses an "insertion sort" algorithm.
    Locate the sort 'list input slot' block included in your project, and time it for each length list.
    Length of List Sort Time
    10
    100
    1000
  4. Talk with Your PartnerHow would you describe what happens to the time as the size of the input list gets bigger? Write a hypothesis.

You can classify algorithms by the amount of time they take to run.

  1. Look back at your table for linear search. Confirm that multiplying the list length by ten roughly multiplies the time taken by ten (linear time).
  2. Look back at your table for binary search. Confirm that the search time for each word list is less than for linear search (sublinear time).
  3. Look back at your table for 25,000 integers. Confirm that it takes about the same amount of time regardless of the input (constant time).
  4. Look back at your table for sort. Confirm that multiplying the list length by ten roughly multiplies the time taken by one hundred (quadratic time).

The difference between linear search and binary search can be very important if you're searching in a list of ten million items, but the most important difference in algorithm efficiency is between polynomial time (proportional to any power of the input size) and exponential time.

In an exponential time algorithm, just adding 1 to the input size (n) of a 2n time algorithm doubles the number of steps! So, for example, if the input size is 20, any polynomial time algorithm will be fast enough, but an exponential time algorithm might take many years to finish.

slow down animation, add labels, make exponential graph red, and fix weird hiccups on graphs; image also needs alt-text like what is in commented out text here. --MF, 4/2/19

On the Internet, many people use the word exponential to mean "happening very fast", such as clickbait-headline-example-blah or example-bleh. -some nicer version of, now you know better-
AAP-2.M.2 text before bullets

One reason it's worth learning these categories is to avoid reinventing the wheel. For example, you've learned that if a list is sorted you can search it in sublinear time using binary search. So when you're writing a program that needs to search through a list repeatedly, it's worthwhile to sort the list before searching. Knowing about algorithms that already exist can help you construct new algorithms.

All of the algorithms you've explored so far in this lab (linear search; binary search; 25,000 integers; and sort) are reasonable time algorithms. The following optional activity is an example of an exponential time algorithm.

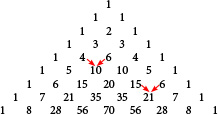
    A problem that may be familiar that requires an exponential time algorithm is computing any given element of Pascal's Triangle. In Pascal's Triangle, each number is found by adding the two numbers above it. For example, 4 + 6 = 10 and 15 + 6 = 21 as shown below. The first and last number of each row, which don't have two numbers above them are 1.
    1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 pascals triangle, row: (6) position (3) reporting 10

  1. Locate the pascals triangle, row: () position: () block included in your project, and time it for various inputs.
    If these take too long to run, you can stop your program; just fill in the table as far as the speed of your computer will allow.
    Inputs Pascal's Triangle Time
    5, 2
    10, 5
    15, 7
    20, 10
    25, 12
    The row value is the input to pascals triangle that matters. (The position input is only given so you get a time for one of the positions near the middle of the row, which take longer to compute.)

    These row inputs are very small compared to the input size for the linear search, binary search, and sort algorithms, and yet the time required for pascals triangle is much higher. Your computer probably can't do much past 25.

    This algorithm works by adding the two numbers above using the algorithm inside itself recursively, but there are better algorithms that compute the value a number in Pascal's Triangle in linear time.
    AAP-4.A part a
  1. Write a paragraph explaining the difference between algorithms that run in a reasonable time and those that do not.
  2. This question is similar to those you will see on the AP CSP exam.
    The table below shows the computer time it takes to complete various tasks on the data of different sized towns.

    Task Small Town
    (population 1,000)    		 Mid-sized Town
    (population 10,000)    		 Large Town
    (population 100,000)
    Entering Data 2 hours 20 hours 200 hours
    Backing up Data 0.5 hours 5 hours 50 hours
    Searching through Data 5 hours 15 hours 25 hours
    Sorting Data 0.01 hour 1 hour 100 hours

    Based on the information in the table, which of the following tasks is likely to take the longest amount of time when scaled up for a city of population 1,000,000.
    Entering data
    Backing up data
    Searching through data
    Sorting data