Proyecto de propagación de enfermedades

En esta página, modelarás la propagación de una enfermedad en una población.

Simulación de una enfermedad que se propaga en una población. Un solo individuo infectado eventualmente hace que todos se infecten.

Nota: Hubo una simulación de propagación de enfermedades en BJC mucho antes del COVID-19, pero queremos reconocer que en este momento la propagación de una enfermedad no es una cuestión abstracta. Todos han sido afectados por el aislamiento en casa, y algunos estudiantes pueden haber perdido a seres queridos a causa de esta enfermedad. Los investigadores médicos utilizan simulaciones (mucho más complejas que esta) para intentar predecir el curso futuro de la enfermedad.

Supongamos que eres un investigador médico de los Centros para el Control y la Prevención de Enfermedades y quisieras entender los factores que contribuyen a la propagación de una nueva enfermedad. En particular, deseas saber el efecto del tamaño de la población en el tiempo que le toma infectarse a cada individuo.

  1. Habla con tu compañero ¿Cuál sería una hipótesis sensata sobre cómo el tamaño de la población afecta al tiempo transcurrido?
  2. ¿Y si el espacio en el que vivía la gente (en la simulación, el tamaño del escenario de Snap!) fuera el doble de grande?

Es posible que no tengas suficientes datos de los brotes reales para probar tu hipótesis y sacar conclusiones significativas, y no sería ético inducir la enfermedad en una población solo para recoger nuevos datos. En esta situación, una simulación sería la mejor opción para generar datos para probar tu hipótesis sin las limitaciones de tiempo, costo y ética.

  1. Haz clic para cargar un proyecto nuevo. Entonces guárdalo.
    Este proyecto incluye:
    • una variable población que almacene el número total de personas (representadas por clones de un objeto)
    • una variable porcentaje infectado inicialmente que almacene la fracción de la población que está enferma al comienzo de la simulación
    • una variable velocidad que almacene el ritmo al que se mueven los clones
    • una variable ¿objetos listos? que almacene un booleano que rastree si todos los clones han sido creados o no y si la simulación puede comenzar
    • una variable número infectados que rastree cuántos clones están infectados en este momento
    • una variable objeto local ¿infectado? que almacene un booleano que rastree si un clon está enfermo o no (cada clon tendrá su propia variable separada con ese nombre)
    • dos disfraces, enfermo (disfraz de objeto 'enfermo': a una pequeña persona roja) y saludable ('disfraz de objeto 'saludable': una pequeña persona azul), que muestran el estatus de cada clon

        • Aprendiste a clonar un objeto en  Unidad 3 Laboratorio 1 Página 5: Construir un tablero de tres en línea.

        El bloque primitivo mis (vecinos) reporta una lista de objetos que están cerca del objeto que lo usa.

        una función simular enfermedad para que la completes que toma tres entradas: población total, porcentaje infectado inicialmente y velocidad del objeto; crea los clones que activan la simulación; y que tenga como salida el tiempo que le toma infectarse a toda la población
      • un bloque iniciar simulación que inicie las variables globales y fije el disfraz padre del objeto
      • un predicado ¿tocando persona infectada? para que lo completes que verifique si el clon actual está siendo expuesto a la enfermedad
      • un bloque iniciar clon que decida si un clon comenzará enfermo y sus posiciones aleatorias en el escenario/li>
      • un guion cuando comienzo como clon para que lo completes que mueva los clones hasta que todos estén infectados
  2. Completa la función simular enfermedad, el predicado ¿tocando persona infectada? y el guion cuando comienzo como clon.
  3. Habla con tu compañero Discute las similitudes y diferencias entre tu simulación y un brote de enfermedad de la vida real. Identifica la simplificación de supuestos que hiciste en la simulación.

Necesitas saber el efecto del tamaño de la población en el tiempo transcurrido. Ya que existe algo de aleatoriedad en la simulación, vas a obtener alguna variación en el tiempo reportado. (Esto no es un error; en la vida real, los eventos aleatorios afectan el tiempo transcurrido).

    AAP-3.F.8
  1. Escribe una función que tome el tamaño de la población como entrada, que ejecute la simulación 10 veces mientras, mantenga el porcentaje de infectados inicialmente en 10 y la velocidad de infección en 2, y reporte el tiempo promedio transcurrido.
    Tiempo medio de propagación de la enfermedad con el tamaño de la población: ()
    2. AAP-3.F.7
  2. Llama a esta función cuatro veces con diferentes poblaciones (50, 100, 150 y 200) y anota los resultados. Crea una hipótesis más definida sobre la relación entre el tamaño de la población y el tiempo para toda la población que se va a infectar.
  3. En los escenarios de enfermedades reales, no todo el mundo acaba enfermando. ¿Cómo decidirías si las simplificaciones que utilizaste en una simulación invalidan las conclusiones que podrías obtener?
    4. El uso de clones es una forma de paralelismo. Pero como aprendiste en la Unidad 5 Laboratorio 1 Página 8: Paralelismo, porque los clones se ejecutan en un solo procesador, la clonación no te hace ir más rápido.

Este es un modelo simplificado. Hay muchas cosas que puedes hacer para que el modelo sea más realista. Por ejemplo, podrías hacer que las personas infectadas se curen con el tiempo, o podrías añadir objetos médicos que puedan curar a los objetos enfermos, pero siempre tendrás que hacer alguna simplificación.

  1. Ahora realiza un experimento similar manteniendo constante el tamaño de la población y variando el porcentaje inicialmente infectado. Plantea una hipótesis para esta relación.
  2. A continuación, realiza otro experimento variando la velocidad de movimiento y manteniendo constantes el tamaño y el porcentaje de la población inicialmente infectada, y crea una tercera hipótesis.
  3. Agrega algunas entradas más al bloque de simulación. Hemos sugerido que la gente mejore después de un tiempo o que se cure por los médicos, pero hay muchas más que podrías pensar.
  4. Tienes hipótesis para cambiar solo una variable, pero ¿qué pasa si cambias dos cosas? ¿Afectan al resultado de forma independiente, o hay un efecto cruzado (por ejemplo, si las personas enfermas se curan rápidamente, ¿cambia esto la relación entre el tamaño de la población y el tiempo transcurrido)? Ejecuta experimentos para averiguarlo.
  5. Diseña e implementa una simulación de predador-presa en Snap!. Por ejemplo, podrías modelar un ambiente con poblaciones de lobos y ciervos donde el lobo se alimenta de los ciervos. ¿Cuáles son algunos de los parámetros que necesitas incorporar en tu modelo para poder simular fluctuaciones realistas en las poblaciones de depredadores y presas?
  6. Imagina que trabajas en un banco que quiere minimizar los tiempos de espera de los clientes en la fila. El banco está considerando dos alternativas:
    • una sola fila donde los clientes se paran en orden de llegada y esperan al siguiente cajero disponible, o
    • filas separadas para cada cajero.
    Diseña e implementa dos simulaciones en Snap! para ayudar al banco a determinar promedio de tiempo de espera para los clientes en cada escenario con el fin de elegir la mejor opción.
    Fila únicaVarias filas
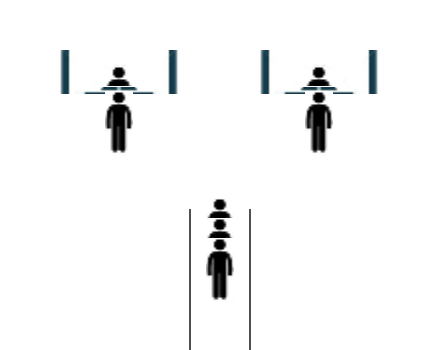
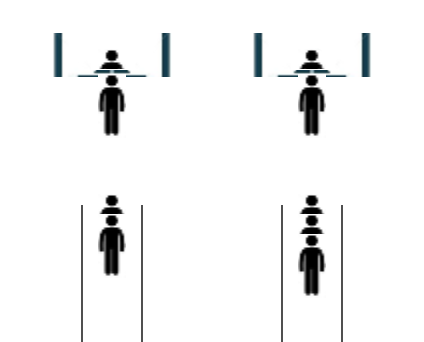
  7. Investiga un poco: ¿Por qué los bancos (la mayoría) utilizan una única fila, pero las tiendas de alimentación (la mayoría) tienen una fila para cada caja?