porque .es.png "redondear (7.5)")
reporta un valor.PG: This is a lovely piece of logic, well written. I'd love to keep it (and see if we can simplify writing even further), but reasoning by contradiction is notoriously hard in all contexts (though, perhaps, page 1 sets it up well enough?) and it isn't obvious that doing it in a programming context would be easier. In fact, the unfamiliarity and extra layer of technicality might make it harder. Do we have any feedback? All this said, CB insists on "teaching this," so the question is how we can make more than an empty factoid out of it. I like our approach. Does it work?
BH: But FYTD 1c is kinda TIFfy. And, I think Church actually proved it before Turing, but we should check. And, bring back his picture!
MF: I want to review this page just because the idea deserves it
En esta página, considerarás un problema que no puede tener una respuesta.
En este punto del curso, has experimentado la frustración de depurar un programa. Sería genial si hubiera un programa de depuración de propósito general que pudiera leer cualquier código y determinar si había errores. Desafortunadamente, podemos usar prueba por contradicción (como hicieron Morgan, Jasmine y Omar en la página anterior) para demostrar que esto no se puede hacer.
Primero, asumiremos que es posible escribir una función para determinar si hay bucles infinitos en un programa (situaciones en las que una función se ejecuta para siempre sin devolver un valor). Luego, utilizaremos esa función en un programa especialmente diseñado para crear una contradicción (una incompatibilidad lógica) para demostrar que la suposición es incorrecta—no puede existir un programa de depuración de uso general. "Este programa tiene errores" es un problema indecidible; nunca se puede construir un algoritmo que siempre lo resuelva correctamente para cada programa.
Un bucle infinito (infinite loop) es una secuencia de instrucciones de computadora que se repite para siempre.
Un problema irresoluble (unsolvable problem) es aquel para el que nunca se puede escribir un algoritmo para encontrar la solución.
Un problema indecidible (undecidable problem) es aquel para el que nunca se puede escribir un algoritmo que siempre dé una decisión verdadero/falso correcta para cada valor de entrada. Los problemas indecidibles son una subcategoría de problemas irresolubles que incluyen solo problemas que deberían tener una respuesta sí/no (como: ¿mi código tiene un error?).
¿detener?
¿detener?; estamos demostrando que no se puede escribir en absoluto, sin importar qué código lo implemente.¿detener? que determina si dado un reportero reportará un valor en un tiempo finito. (Si es así, decimos que el reportero se detiene.) Se necesitan dos entradas: una función y un valor de entrada para esa función. Reporta verdadero si la función reportase un valor cuando se le da esa entrada; y reporta falso si la función se ejecutase para siempre (en un bucle infinito).
Por ejemplo, la función redondear no se ejecutará para siempre cuando se le dé la entrada 7.5; reportará 8.
¿detener? tratará la función de entrada como datos en lugar de ejecutarla. porque reporta un valor.
Por otro lado, imagina que tenemos una función que se atascará en un bucle infinito cuando se le dé la entrada foo; nunca reportara (nunca se detendra).
porque .es.png "programa con un bucle infinito (foo)")
bucles infinitamente.
Usaremos prueba por contradicción para mostrar que la siguiente pregunta no se puede responderen general:
¿Un determinado programa de computadora, dada una determinada entrada, reportara un resultado en un tiempo finito?
El "programa de computadora" es la primera entrada para ¿detener?. La "entrada dada" es la segunda entrada para ¿detener?. Y lo qué ¿detener? reporta es verdadero o falso: si el "programa de computadora" se detendrá o no.
Tenga en cuenta que ¿detener? siempre debe reportar un resultado, incluso si el programa que está probando no lo hace. Esto se debe a que estamos asumiendo (una suposición que mostraremos es falsa) que ¿detener? siempre funciona—que siempre reporta una respuesta.
Podemos responder esta pregunta para algunas funciones específicas, pero estamos tratando de determinar si podemos idear una prueba general que nos diga si alguna función particular reportará un valor para alguna entrada específica.
La parte "en general" es importante. Por supuesto, podemos responder la pregunta para ciertos programas particulares. Éste se detiene (reporta un valor) para cualquier entrada:
Este nunca se detiene para cualquier entrada:
Y este se detiene a veces—para cualquier entrada excepto 87:
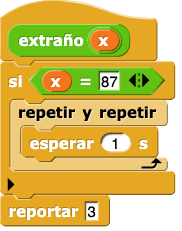
Recuerda: la pregunta es si podemos idear una prueba que nos dirá si alguna función particular reportará un valor para cualquier entrada específica.
¿detener?.¿detener? en este proceso de prueba por contradicción.¿detener? no funcionará
Para demostrar que no puede existir tal función, necesitamos crear una contradicción. Necesitamos demostrar que tiene que haber al menos una función y una entrada a esa función para la cual ¿detener? no funciona de la manera que asumimos. Por lo tanto, podemos hacer un bloque prueba, específicamente con el propósito de romper ¿detener?:
# y ⋮ para las entradas declaradas como números o listas, el λ no forma parte del nombre de la entrada, pero es una sugerencia de tipo que se creó al seleccionar el tipo de entrada reportero:
prueba tendrá un anillo gris redondeado para indicar que la entrada debe ser un reportero: .es.png "prueba ()")
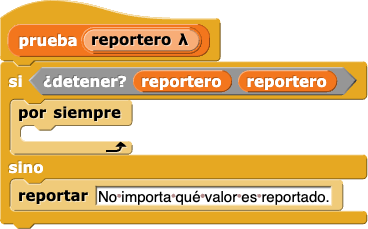
El bloque por siempre en este script crea un bucle infinito. Si el código de prueba termina en esta parte de la declaración si, nunca reportara nada. Entonces, entonces si prueba se detendrá el mismo depende de la salida del predicado ¿detener? en la declaración si dentro de él.
La expresion 
pregunta qué sucederá si llamamos a la función de entrada (reportar) con el mismo como su propia entrada. Esto es similar a cuando Jasmine hizo una declaración sobre la declaración que estaba haciendo, cuando dijo: "La declaración que estoy haciendo en este momento es falsa".
Este es desafiante. ¡Quédate con eso! Estamos creando una contradicción para demostrar que no puede existir la función ¿detener? a la que se llama dentro de prueba.
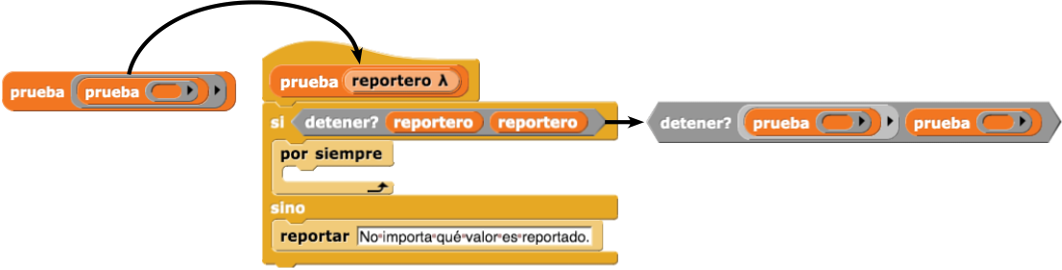
Para hacer que la situación sea exactamente como lo que dijo Jasmine ("La declaración que estoy haciendo en este momento es falsa"), llamaremos a prueba dentro de sí mismo:
Ahora, la instrucción si dentro del bloque prueba preguntará si prueba se detendrá (no se ejecutará para siempre) si se llama con prueba como su entrada. El predicado en la instrucción si se convertirá en ¿detener? (prueba) (prueba).
Entonces, al igual que en los ejemplos anteriores,
significaría que devuelve un valor.
significaría que bucles infinitamente.
Cuando llamamos , nos encontramos con la contradicción. Para ver cómo, mire hacia atrás en la definición de prueba:
Mostrar que el resultado tiene que estar equivocado implica un análisis de casos como los utilizados para resolver los acertijos lógicos en la página 1. Considera los dos casos posibles:
entonces prueba tomará la primera parte del si, por lo que se repetirá para siempre. Eso significa no se detendrá, ¿entonces ¿detener? dio la respuesta incorrecta. entonces prueba tomará la parte sino y reportará "No importa qué valor se reporte". Eso significa que se detendrá, por lo que ¿detener? vuelve a estar equivocado. prueba reporta, solo que reporta algún valor, pero sí importa qué valor reporta ¿detener?.No importa lo que reporte ¿detener?, siempre estará en desacuerdo consigo mismo en un programa como este. Esta contradicción (esta imposibilidad lógica) significa que la suposición de que es posible escribir ¿detener? tiene que estar equivocada. Esto no es solo un reclamo sobre lo que sucederá en Snap!. El lenguaje que uses para explorar un problema computacional puede afectar la claridad o la legibilidad de tu código, pero no si existe una solución a un problema. Incluso con los avances en computación cuántica, nunca podremos crear un programa de depuración de propósito general. Este famoso ejemplo se conoce como el problema de detención y el hecho de que el problema de detención no sea decidible es el Teorema de detención.
Revisen toda esta prueba nuevamente juntos. Asegúrate que tanto tú como tu pareja entiendan:
¿detener? y cómo funciona.prueba (para cualquier función de entrada) conduce a una contradicción
Alan Turing (1912–1954) fue un científico de la computación y matemático británico. Durante la Segunda Guerra Mundial, desarrolló una serie de tecnologías críticas para descifrar mensajes alemanes encriptados, desempeñando un papel clave en ayudar a las fuerzas aliadas a derrotar a los nazis. Mientras trabajaba en la Universidad de Manchester después de la guerra, dedicó más tiempo a la idea de la Inteligencia Artificial, proponiendo lo que ahora se conoce como el "Test de Turing". Junto a su colega, Alonzo Church, Turing fue uno de los fundadores de la ciencia de la computación teórica, demostrando que las computadoras deben funcionar independientemente de la tecnología futura.
Demostró que existen problemas matemáticos bien definidos que las computadoras nunca pueden resolver, sin importar lo grande y rápido que sean. Trágicamente, Turing fue procesado por "indecencia" cuando las autoridades descubrieron que era homosexual, y se sospecha que se suicidó después de ser sometido a tratamientos hormonales. A menudo se le considera el "padre de la computación moderna".