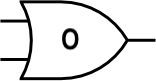
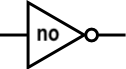
Y, O, y NO:
y, o y no) y aprenderás cómo se relacionan con los circuitos electrónicos.En un circuito con miles de millones de transistores, o incluso miles de transistores, los diseñadores de hardware no pueden pensar en cada transistor individual. Del mismo modo que los programadores usan la abstracción, los arquitectos de hardware usan abstracciones, en las que un grupo de transistores y otros elementos del circuito se consideran una sola cosa. ¿Qué tipo de cosas? Básicamente hay dos tipos, uno para la memoria y otro para el cálculo.
La memoria está hecha de flip-flops. Un flip-flop es un circuito que tiene dos estados estables, encendido y apagado. Una señal de entrada puede indicarle que se encienda, apague o cambie su estado. Una vez que eso sucede, el flip-flop permanece en el nuevo estado hasta que recibe otra señal. Tiene una salida que refleja su estado: encendido si el flip-flopp está encendido, apagado si está apagado.
Los circuitos para hacer cálculos son más interesantes. Estos calculan funciones, al igual que los reporteros en Snap!. Dado que las computadoras hacen mucha aritmética, podrías pensar que los circuitos básicos de funciones serían la suma, la resta, la multiplicación y la división, pero ese no es el caso. Por supuesto, hay circuitos para hacer esas cosas, pero están hechos de compuertas lógicas: circuitos que calculan funciones booleanas: y, o y no.
La razón por la que las funciones booleanas se consideran más fundamentales es que sus entradas y salidas se pueden representar con un solo cable que entra o sale del circuito. Eso no es así en las funciones aritméticas. Si consideras que un voltaje en un cable significa 1, y ningún voltaje significa 0, entonces debes ver que un sumador tendrá tres posibles valores de salida, porque 1+1=2, que no es ni 0 ni 1. Por el contrario, si considera que un voltaje en un cable significa Verdadero y ningún voltaje significa Falso, entonces la salida de una función booleana de dos entradas solo puede ser Verdadero o Falso, por lo que solo se necesita un cable de salida.
Viste algunos ejemplos en Unidad 2 Laboratorio 3: ¿Qué es un predicado?: Y, O, y NO:
y.
Este circuito eléctrico muestra una forma simplificada de emular el operador booleano y electrónicamente. Los dos interruptores están en serie; si ambos interruptores están encendidos, la corriente fluye y la bombilla se enciende.
| entradas | salida | |
|---|---|---|
| A | B | A y B |
| Falso | Falso | Falso |
| Falso | Verdadero | Falso |
| Verdadero | Falso | Falso |
| Verdadero | Verdadero | Verdadero |
| entradas | salida | |
|---|---|---|
| A | B | A y B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
o.
Este circuito eléctrico muestra una forma simplificada de emular el operador booleano o electrónicamente. Los dos interruptores están en paralelo; Si cualquiera (o ambos) de los interruptores están encendidos, la corriente fluye y la bombilla se enciende.
Al igual que con las tablas y, Estas dos tablas son idénticas, excepto en si usan verdadero/falso o unos/ceros.
En el lenguaje ordinario, la palabra "o" puede tener dos significados ligeramente diferentes. o inclusivo significa "al menos uno de estos": si está lloviendo o hace mucho frío, necesitas tu abrigo. (Si llueve y hace frío, igual usarías el abrigo.) o exclusivo significa "esto o aquello, pero no ambos": Come tus verduras o no obtendrás ningún postre. (Te sentirías engañado si comieras las verduras y aún no recibieras el postre.) En computación (como en matemáticas) la palabra "o" por sí mismo siempre significa un o inclusivo, como puede ver en esta tabla de verdad. Si te refieres a "o exclusivo," tienes que decirlo
| entradas | salida | |
|---|---|---|
| A | B | A o B |
| Falso | Falso | Falso |
| Falso | Verdadero | Verdadero |
| Verdadero | Falso | Verdadero |
| Verdadero | Verdadero | Verdadero |
| entradas | salida | |
|---|---|---|
| A | B | A o B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
no.
Este circuito eléctrico muestra una forma simplificada de emular el operador booleano. no electrónicamente. Este interruptor es básicamente un disyuntor: si el interruptor está encendido, el flujo de corriente se interrumpe y la bombilla se apaga; Si el interruptor está apagado, la corriente fluye directamente a la bombilla y la bombilla se enciende.
| entrada | salida |
|---|---|
| A | no A |
| Falso | Verdadero |
| Verdadero | Falso |
| entrada | salida |
|---|---|
| A | no A |
| 0 | 1 |
| 1 | 0 |
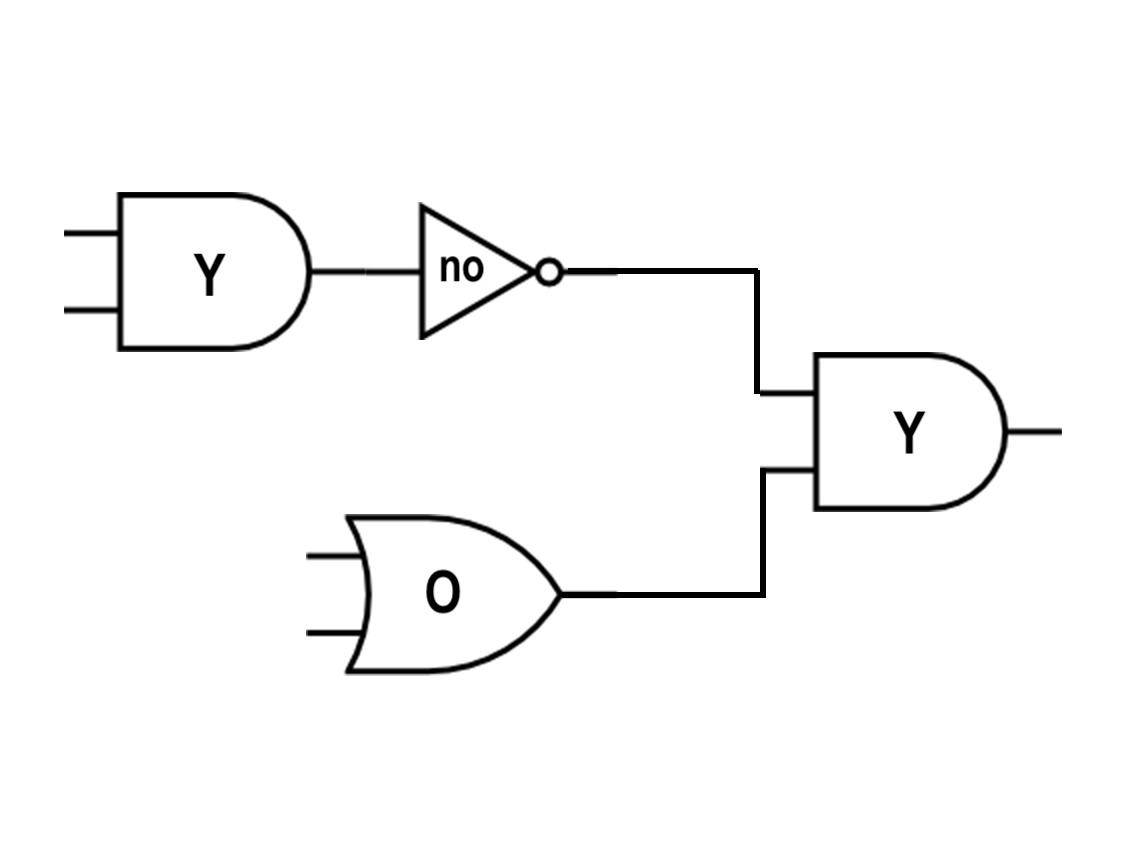
Dentro de una computadora, las operaciones booleanas se implementan en circuitos físicos utilizando compuertas lógicas. (Una sola compuerta implementa una de las funciones básicas y, o o no.) Los circuitos lógicos a menudo se representan con dibujos que ayudan a los ingenieros a ver cómo fluirá la información a través de un circuito. Por ejemplo, el siguiente diagrama de un circuito lógico con dos compuertas representa la expresión booleana or((a)and(b))-booleans.es.png "A o (A y B)")
. ¿Puedes ver cómo?
or((a)and(b))-gate.es.png "diagrama de compuerta lógica de (A o (A y B))")
Mira el circuito lógico dibujado arriba. ¿Para qué valores de A y B la salida será verdadero?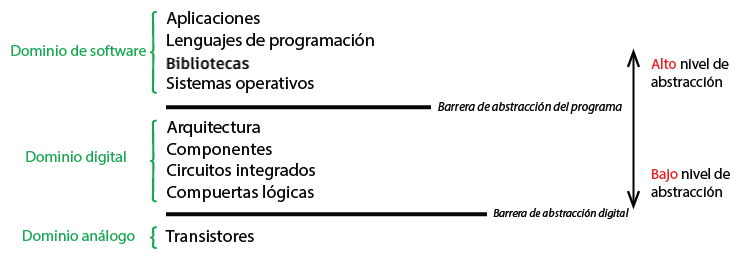
y, o, y no con las siguientes preguntas, que son similares al tipo de preguntas que verás en el examen AP CSP.
verdadero?
(verdadero) y (falso). ¿Qué reporta? no((verdadero) y (falso)). En la expresión II: ¿Qué reporta? (verdadero) o (falso). ¿Qué reporta? no((verdadero) o (falso)).no((verdadero) y (falso)) (a la derecha) al bloque y externo?(verdadero) y (falso) (a la derecha) al bloque o externo?verdadero? (T representa Verdadero y F representa falso.)
|
|
|
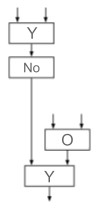Los ingenieros generalmente dibujan compuertas lógicas horizontalmente y usan formas especiales que representan cada compuerta:
