Binary Addition with Logic Gates

On this page, you will catch a glimpse of how computers do basic arithmetic operations such as addition using only binary digits and logic gates.

Review: Addition of numbers

When you add two numbers in the decimal system (base 10) you evaluate each column of addition by taking into consideration any carry in value from the previous column and then passing on to the next column any carry out value.


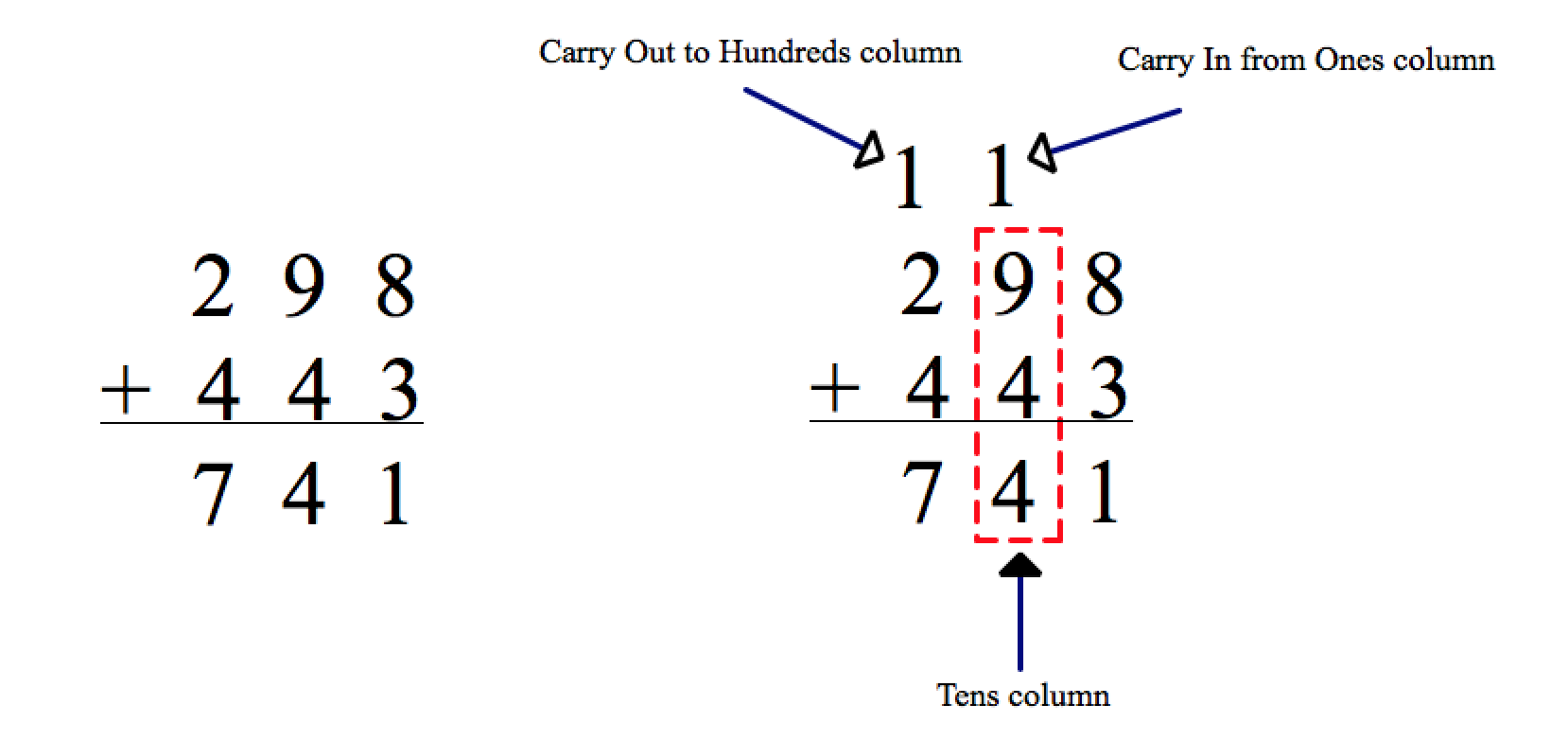
The exact same procedure is followed when you add two numbers in the binary system (base 2) as shown below.


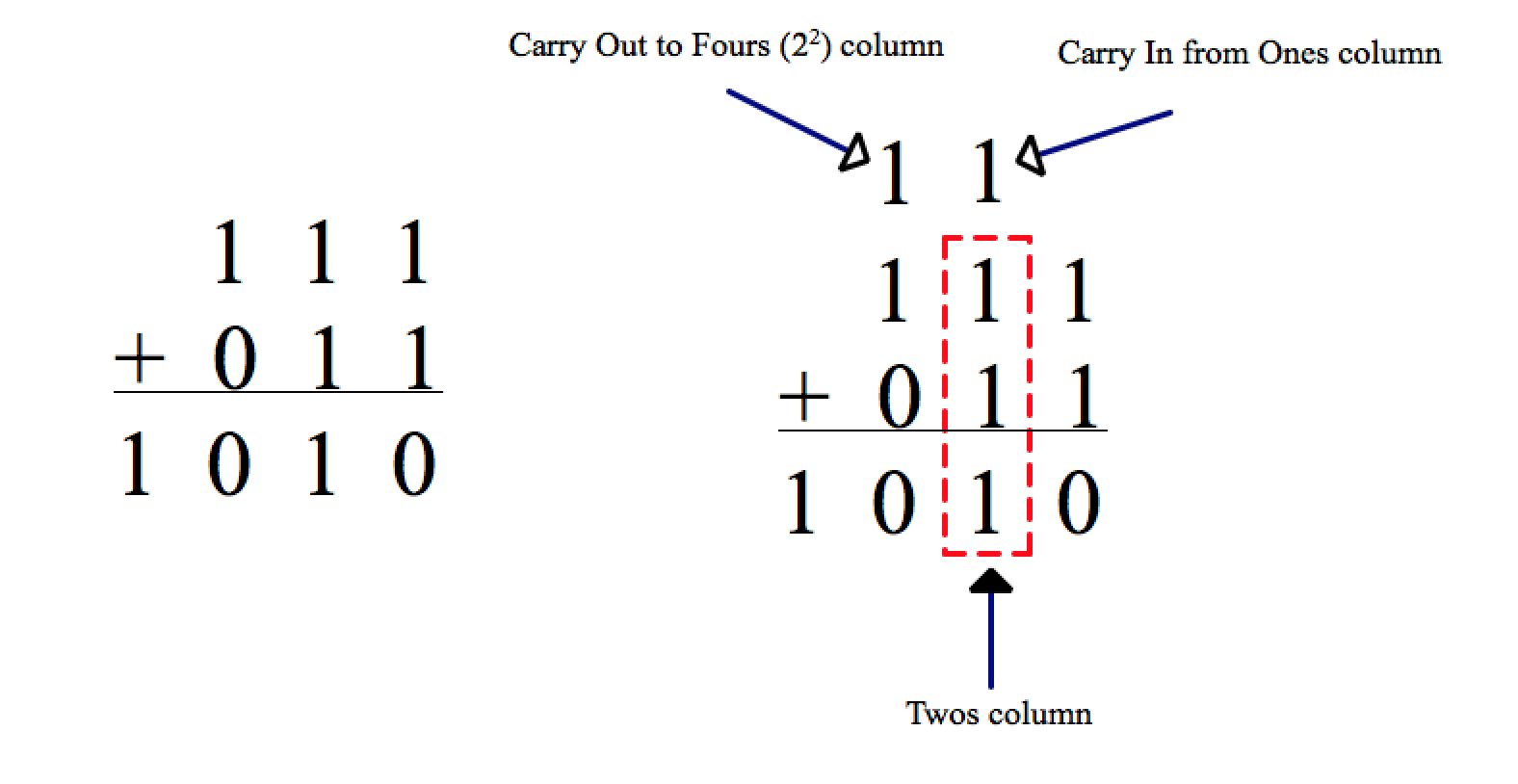
As you can see in order to perform the addition of numbers you must be able to accomodate inputting a carry in value and outputting a carry out value.

Half-Adder

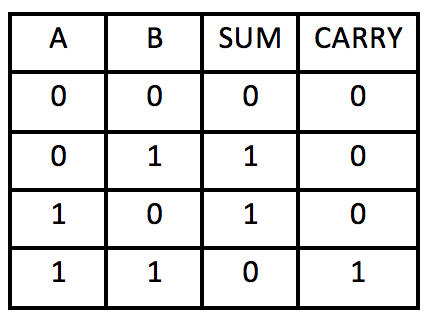
A half-adder adds two binary digits (with no carry in) and reports the sum and the carry out value. If you look at the "SUM" column you will notice that it is identical to the output column of XOR and if you look at the "CARRY" column you will notice that it is identical to the output column of AND.

If you are having difficulty making sense of this table consider addition of binary digits:
0+0=0
0+1=1
1+0=1
1+1=2 which is 10 in binary with a units digit sum of 0 and a carry of 1.
Half-Adder table with Sum and Carry
Half-Adder
  1. Click here to load a starter project. Then save it.
  2. Examine the Snap! file and all its sprites. For the sprites SUM and CARRY assemble some code blocks to emulate a half-adder.

Full-Adder

If you are having difficulty making sense of this table consider addition of three binary digits:
Sum of three bits
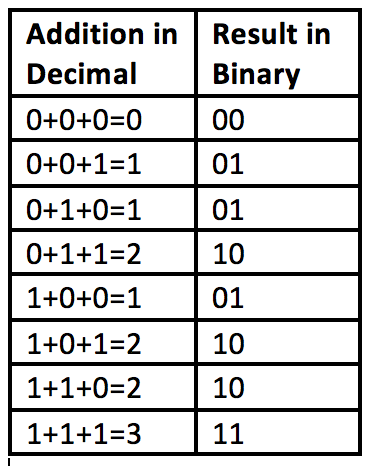
For example, 1+1+1=3 which is 11 in binary with a ones digit of 1 and a carry out value of 1.

A full-adder uses two half-adders to perform a full addition of binary digits accomodating a carry in value. It reports the sum and carry out value.

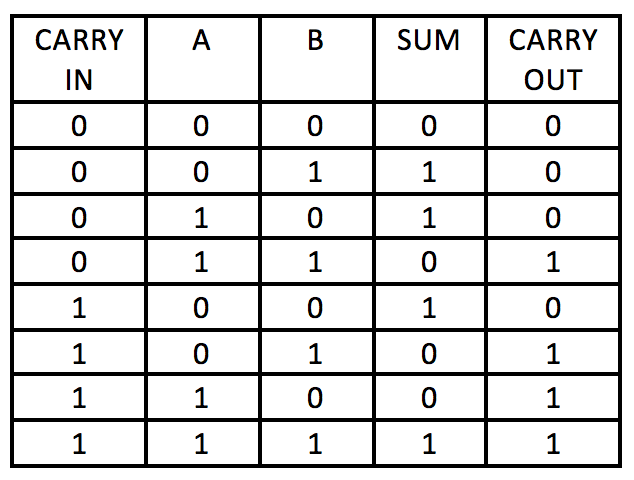
Full-Adder table with Carry In, Sum, Carry Out
Full-Adder
  1. Study the table and the full-adder schematic given above to explain how the full-adder performs the addition of two binary numbers with a carry in using two half-adders and an OR gate.
  2. Click here to load a starter project. Then save it.
  3. Examine the Snap! file and all its sprites. Code for sprites CARRY IN, A and B, have been written for you. For the sprites SUM1, CARRY1, SUM OUT, CARRY2, CARRY OUT, assemble some code blocks to emulate a full-adder.
  1. Learn about ripple carry adders and explain how they use full-adders to add multi-digit binary numbers. Build a Snap! program to emulate the addition of two 4-digit binary numbers with a ripple carry adder.
    Image Credit: Wikipedia user Cburnett
  2. Learn how computers subtract and multiply binary numbers using logic gates and build Snap! programs to emulate these operations.