Building a Binary Adder

On this page, you explore how logic gates can be combined to perform arithmetic (specifically, addition) with binary values.

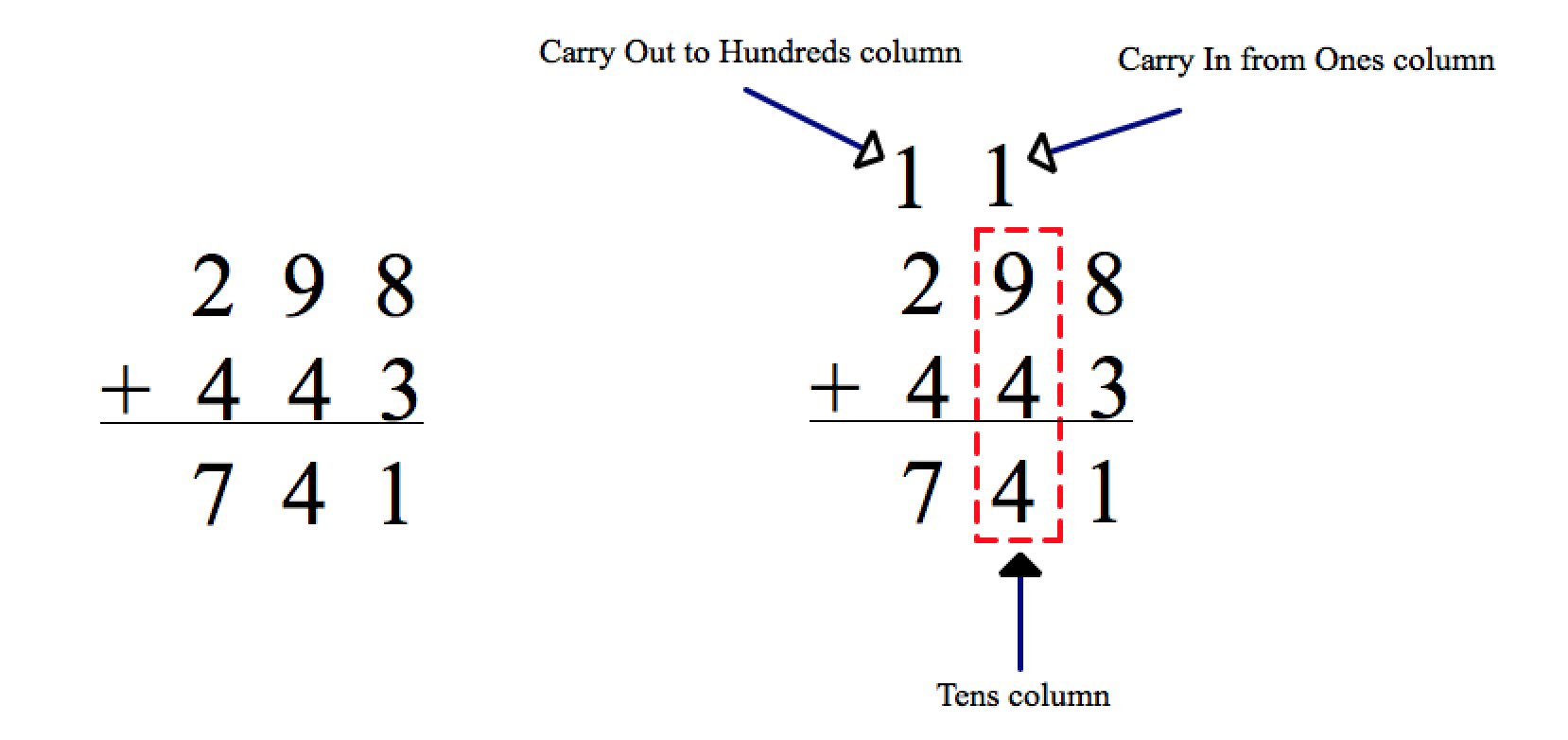
Recall that when you add two numbers (in base 10), you find the sum of each column including any carried value from the previous column.

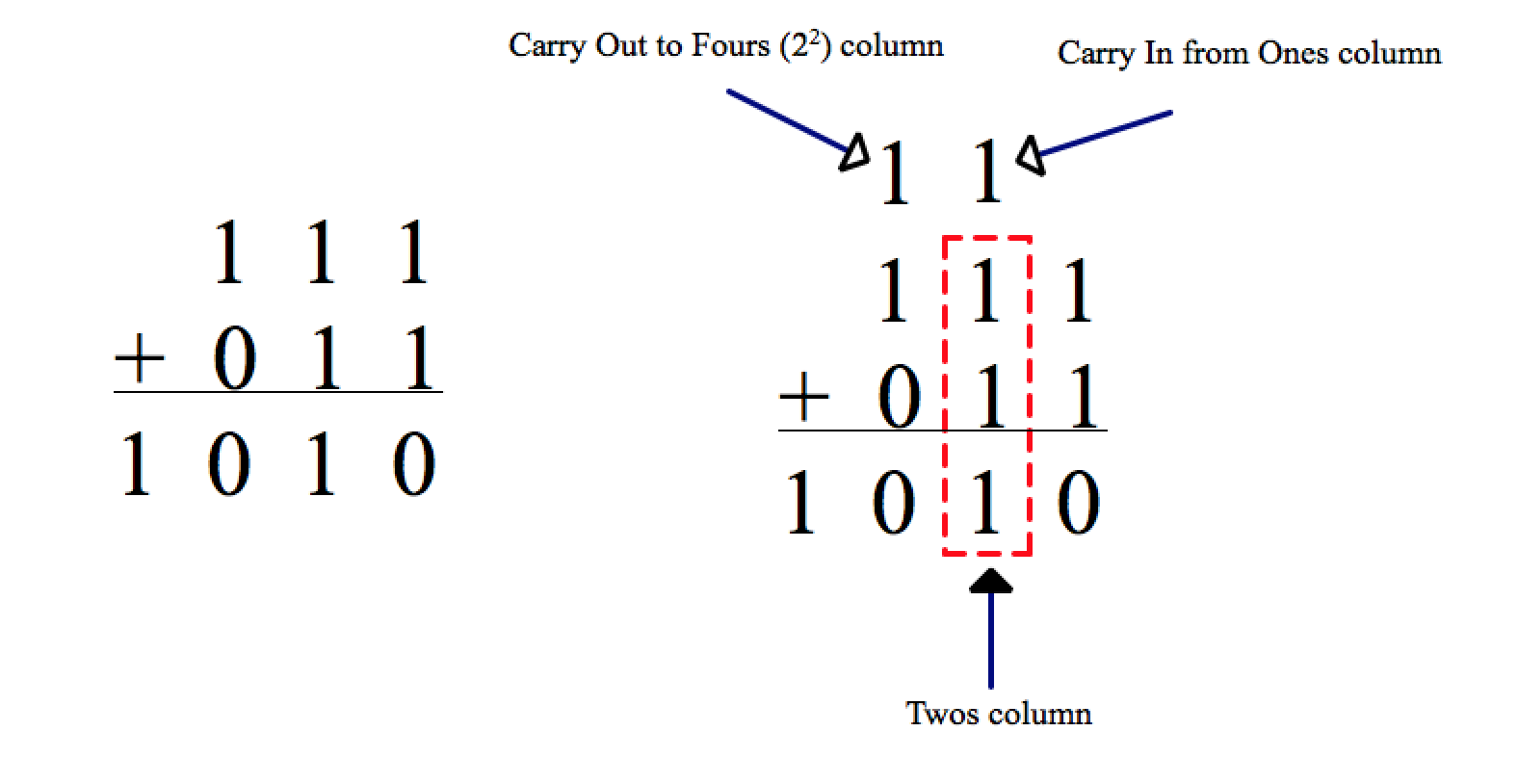
Need new, clearer, simpler image with only the right side and only "carry" not carry in/carry out.

Need new, clearer, simpler image with only the right side and only "carry" not carry in/carry out.

The same procedure is used to add two numbers in base 2.


In order to perform addition, any algorithm must accomodate values carried over from lower place values to higher place values.

Half-Adder

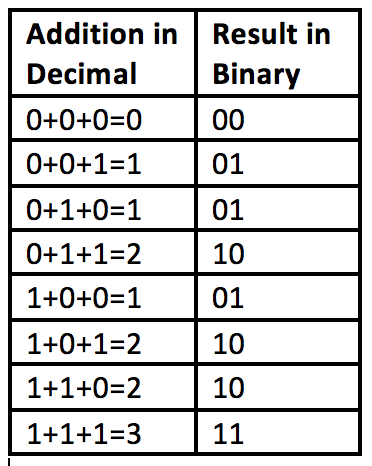
Boolean Operators each take two Boolean values (true or false) as input and report a single bit (a single Boolean value) as output. This is unlike the basic operations used in math. For example in addition, the sum of two single-bit values can have a two-bit result: 1 + 1 = 10 in binary. So things like arithmetic circuitry are built out of Boolean circuitry.

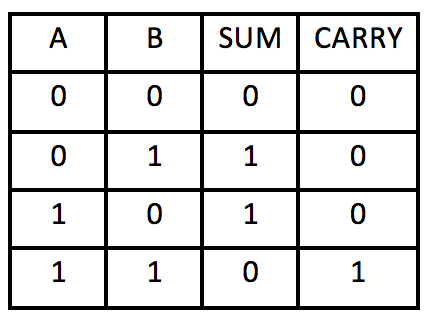
A half-adder adds two binary digits (with no carry in) and reports the sum and the carry out value. If you look at the "SUM" column you will notice that it is identical to the output column of XOR and if you look at the "CARRY" column you will notice that it is identical to the output column of AND.

If you are having difficulty making sense of this table consider addition of binary digits:
0+0=0
0+1=1
1+0=1
1+1=2 which is 10 in binary with a units digit sum of 0 and a carry of 1.
Half-Adder table with Sum and Carry
Half-Adder
  1. Click here to load a starter project. Then save it.
  2. Examine the Snap! file and all its sprites. For the sprites SUM and CARRY assemble some code blocks to emulate a half-adder.

Full-Adder

If you are having difficulty making sense of this table consider addition of three binary digits:
Sum of three bits
For example, 1+1+1=3 which is 11 in binary with a ones digit of 1 and a carry out value of 1.

A full-adder uses two half-adders to perform a full addition of binary digits accomodating a carry in value. It reports the sum and carry out value.

Full-Adder table with Carry In, Sum, Carry Out
Full-Adder
  1. Study the table and the full-adder schematic given above to explain how the full-adder performs the addition of two binary numbers with a carry in using two half-adders and an OR gate.
  2. Click here to load a starter project. Then save it.
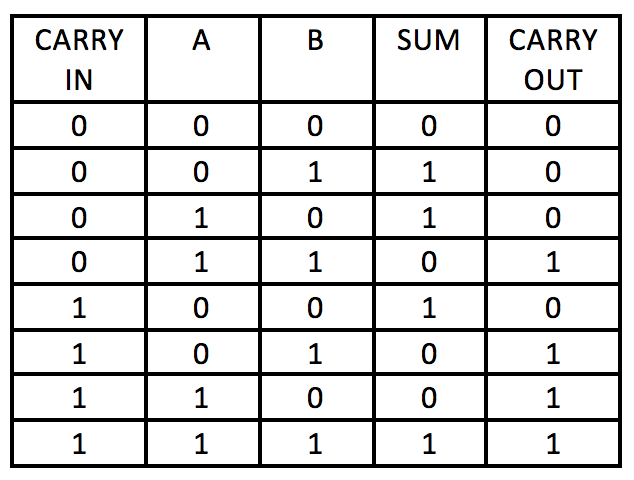
  3. Examine the Snap! file and all its sprites. Code for sprites CARRY IN, A and B, have been written for you. For the sprites SUM1, CARRY1, SUM OUT, CARRY2, CARRY OUT, assemble some code blocks to emulate a full-adder.
  1. Learn about ripple carry adders and explain how they use full-adders to add multi-digit binary numbers. Build a Snap! program to emulate the addition of two 4-digit binary numbers with a ripple carry adder.
    Image Credit: Wikipedia user Cburnett
  2. Learn how computers subtract and multiply binary numbers using logic gates and build Snap! programs to emulate these operations.



Binary addition:

I think this is kind of backwards.  It introduces "carry out" and "carry in" as
technical terms before indicating why they're important, namely, adding more
than one-bit-wide numbers.

1.  Do a base 10 addition that involves carrying, and introduce the idea that,
e.g., the "carry out" from the tens column is the "carry in" to the hundreds
column.

2.  Do the same thing in binary, with the difference that the carry signals are
just a single wire wide.

3.  Show a single-bit slice of the addition to show that the + circuit needs
/three/ inputs and /two/ outputs.

4.  Draw a ripple adder, to show how the Carry Out from one bit slice becomes
the Carry In for the next-left bit slice.

5.  Now you're ready to say that the traditional way to build a one-bit-wide
adder is to start with a circuit called a half-adder that has a carry out but
no carry in.

6.  Draw this picture:

              +----------+
      A ----->|          |-----> Sum
              |half adder|
      B ----->|          |-----> Carry Out
              +----------+

and then /have the students build it!/  No leading them by the nose ring.  If
you must, have a /hidden/ hint that just says "Draw a truth table for Sum and
another truth table for Carry Out."

7.  Show the figure with two half adders cascaded, but leaving out the OR gate
and the three output labels.  Have the students draw the rest of the circuit,
after reminding them that they're supposed to produce two outputs, Sum and
Carry Out.  Also remind them that /each half-adder/ has outputs called Sum and
Carry Out, and that the full adder has its own outputs with the same name, and
all three are distinct.

I think it should say someplace that computers today don't really use these
simple ripple carry circuits because they're too slow; each bit has to wait for
the bit to its right before it can figure out its own output.  So, TIF A:  How
do computers /really/ add binary integers?

TIF B has two parts, each with pitfalls.  To do subtraction, you really have to
first understand twos complement.  As for multiplication, as I said earlier,
there's the simple way (shift and add), and then there's the real way (much
more complicated, involving, I think, table lookup for slices of four or eight
bits).

Half-Adder

A half-adder adds two binary digits and reports the sum and the carry over value. If you look at the "SUM" column you will notice that it is identical to the output column of XOR and if you look at the "CARRY" column you will notice that it is identical to the output column of AND.

If you are having difficulty making sense of this table consider addition of binary digits:
0+0=0
0+1=1
1+0=1
1+1=2 which is 10 in binary with a units digit sum of 0 and a carry of 1.
Half-Adder table with Sum and Carry
Half-Adder
  1. Click here to load a starter project. Then save it.
  2. Examine the Snap! file and all its sprites. For the sprites SUM and CARRY assemble some code blocks to emulate a half-adder.

Full-Adder

If you are having difficulty making sense of this table consider addition of three binary digits:
Sum of three bits
For example, 1+1+1=3 which is 11 in binary with a units digit sum of 1 and a carry of 1.

A full-adder uses two half-adders to perform a full addition of binary digits with a carry in value. It reports the sum and carry out value.

Full-Adder table with Carry In, Sum, Carry Out
Full-Adder
  1. Study the table and the full-adder schematic given above to explain how the full-adder performs the addition of two binary numbers with carry in using two half-adders and an OR gate.
  2. Click here to load a starter project. Then save it.
  3. Examine the Snap! file and all its sprites. Code for sprites CARRY IN, A and B, have been written for you. For the sprites SUM1, CARRY1, SUM OUT, CARRY2, CARRY OUT, assemble some code blocks to emulate a full-adder.
  1. Learn about ripple carry adders and explain how they use full-adders to add multi-digit binary numbers. Build a Snap! program to emulate the addition of two 3-digit binary numbers with a ripple carry adder.
  2. Learn how computers subtract and multiply binary numbers using logic gates and build Snap! programs to emulate these operations.