Recursive Tree
In this lab, you will create a tree-drawing program that uses recursion to draw the branches by drawing smaller and smaller trees.
On this page, you will explore nesting code for trees inside code for trees.
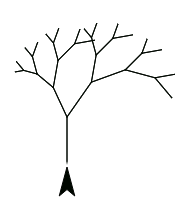
The branching pattern on many plants has fractal structure: the smaller parts are like miniature copies of the whole plant.
:
Fractal
A fractal is an infinite repeating pattern made up of copies (or slight variations) of the same shape. In this picture, the green branch is (essentially) the same shape as the entire picture.
![fractal tree fractal tree]()
:
State Transparency
State transparency means putting everything back exactly as it was when you started. It is especially important when blocks depend on other blocks. Usually, this means returning the sprite to the same position and direction and returning the pen to the same color and size.
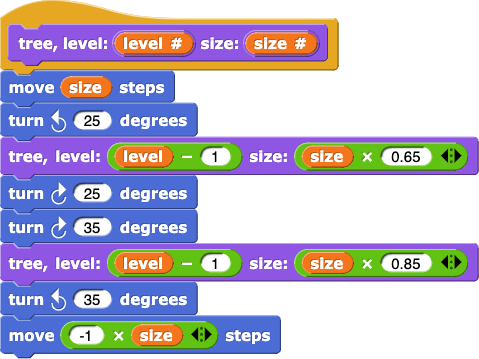
These blocks all look essentially the same except that tree 5 uses tree 4, while tree 4 uses tree 3, and tree 3 uses tree 2, etc. So it makes sense to wonder if we can replace all these blocks with a single tree block by using a variable for the number that changes.
:
Recursion
Using a procedure inside of itself is called recursion.
-
This is the general idea for the recursive version.
 What are the differences between this recursive tree script and the code for
What are the differences between this recursive tree script and the code for tree 2 and tree 3, and why are these differences needed?
-
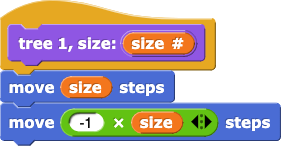
Here is what happens if you run
tree, level: 9 size: 50.
![Tree drawing never terminates, stuck at a single branch Tree drawing never terminates, stuck at a single branch]()
It doesn't work. Try to debug the script. Consider building the code and running it yourself.  What's going wrong?
What's going wrong?

.png) . You should get a result like this:
. You should get a result like this: 
 Where does your sprite start? In what direction is it facing? Where does it stop?
Where does your sprite start? In what direction is it facing? Where does it stop?
.png)

 Describe exactly the position and direction of the sprite when the first
Describe exactly the position and direction of the sprite when the first 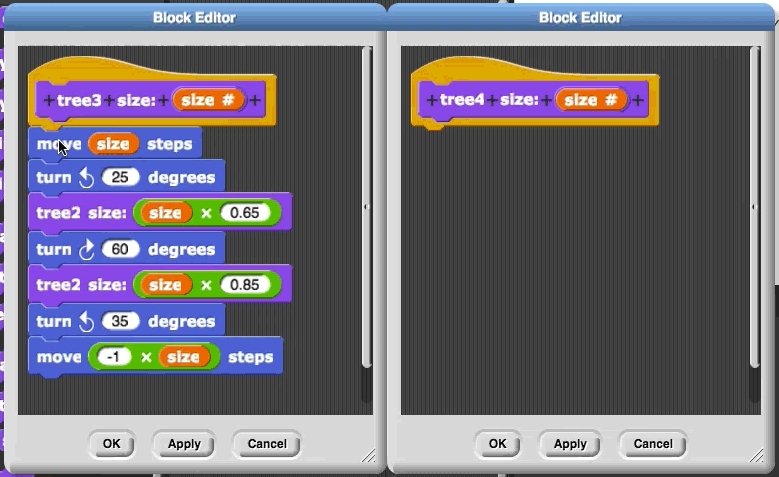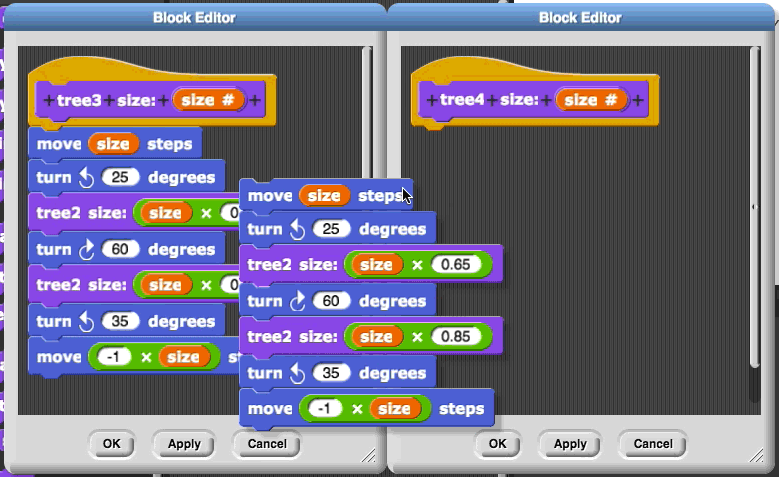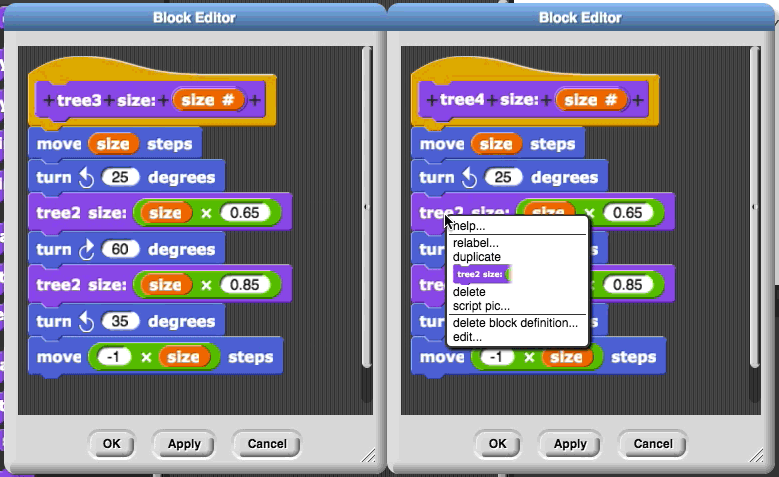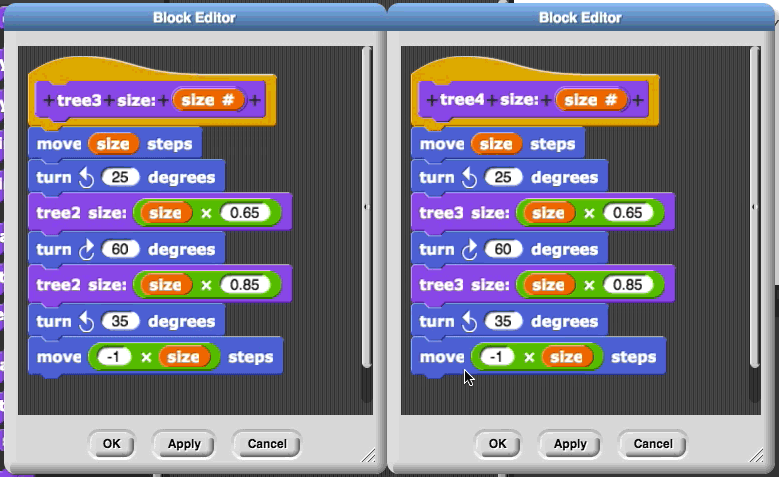
.png) should produce a result like this.
should produce a result like this.