Counting Trees
PG: Generic editing: Beta doesn't have a consistent name. Sometimes Betty, sometimes Jasmine. General comment: I don't feel like we've settled on a goal and really crafted a sequence to reach it. I think we're showing off all sorts of things that can be done with recursion, rather than thinking about how to /teach/ recursion and structuring this so that the student really becomes the master. This page: I basically like this, but I feel it is less focused on helping a kid write a recursive reporter than on the mathematics. Morgan's solution and the first four lines of the TOL are clever but, for our purposes, irrelevant. Worse, if we want to build a power of 2 block, we should teach how to do /that/ recursively. The method here (last two lines of TOL) does, sort of, do that, but because the focus is elsewhere (and we never draw it back), it is likely to be special purpose. We don't see the right abstraction, Morgan's "one less than a power of 2."
BH to sort out this feedback from Tim Matthies : Post2 --MF, 6/17/20
Mary to consider: Post1
In this lab, you will develop recursive reporters.
On this page, you will explore a procedure for counting the segments in a fractal tree, and re-build it recursively.
In Unit 7, you built recursive trees. Each tree is made up of line segments.
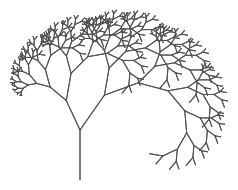
-
Open your "U7L1-Tree" project. How many line segments are in a tree of each level? Complete this table. (You can count by eye or have Snap! count for you.)
| level |
segment count |
| 1 |
1 |
| 2 |
3 |
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
 How does the number of segments in one level compare to the number of segments in the previous level?
How does the number of segments in one level compare to the number of segments in the previous level?- Build a block whose input is a tree number and whose output is the number of segments in that level:

Morgan and Jasmine discuss the code they created.
Morgan: I noticed a pattern in the table. Each number of segments is one less than a power of 2.
Jasmine: What does your code look like?
Morgan: I used a for loop to build the power of 2, then I subtracted 1 at the end:
Morgan: At the end, the report block sends the final value. I put the last math operation there.
Jasmine: Wow. Mine looks a lot different! I made the code look like the code for tree.
Morgan: Interesting... but I don't get it.
Jasmine: Look back at the code for tree. We used recursion. We built a segment, turned, called tree to build a smaller tree, turned again, and then called tree again to build another, smaller tree.
Morgan: Cool! We can think about how that algorithm works to write the segments in tree reporter recursively. But we can ignore all the moving and turning parts, right? Let me give this a shot.
Jasmine: Right! And don't forget: base cases are important!
You've built and worked with recursive command blocks. Recursion can also be used in reporters.
-
If you haven't yet, build a recursive reporter that reports the number of segments in a tree of level n.
Remember that you need to click "Apply" before you can use your block recursively in the Block Editor.
The following is all from a second page and needs to be properly integrated by Mary. --MF, 6/17/20
PG: Drastic change, based on whatever we do with "counting branches" (not trees—there's only one tree), this should change. The reporter is so special-purpose, whereas a n^m block is both /less/ complex (more straightforward) and /more/ generally useful, e.g., for counting the triangle's children.
- I had written n^m into U2 Math Tools, but it's now a primitive. --MF, 4/5/19
Here's Jasmine's code for the segments in tree function:

The report block only connects to the blocks above it. That's because report returns the result of its input slot, immediately, as the output of the segments in tree reporter block. No further code is executed in a reporter after a report block.
Do we need this commented out content? --MF, 6/22/20

 How does the number of segments in one level compare to the number of segments in the previous level?
How does the number of segments in one level compare to the number of segments in the previous level?


