- Escribe todos los subconjuntos de {manzana, naranja, plátano}. ¿Cuántos hay?
- Escribe todos los subconjuntos de {Pretzel, Manzana, Naranja, Banana}. Trate de hacer esto con el menor trabajo posible.
-
Ahora crea un bloque
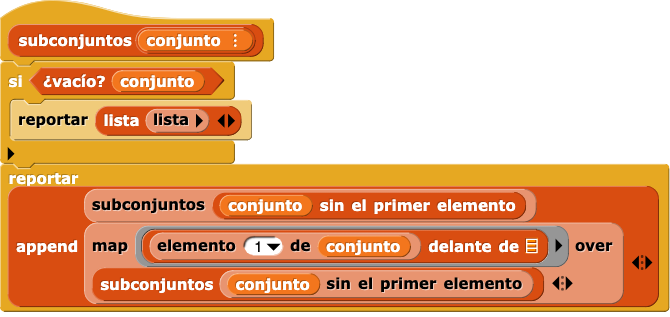
subsetsque toma una lista como entrada y reporta una lista de listas en la que cada elemento es un subconjunto de la lista de entrada original. El orden en que aparecen los subconjuntos en la lista de salida no importa, pero cada subconjunto debe aparecer exactamente una vez. El resultado podría verse así:

Si estás atascado después de probar tantas ideas que se te ocurran, haz clic aquí para obtener un poco de ayuda.
- ¿Cuántos subconjuntos tiene el conjunto vacío {}?
- ¿Qué deberían informar los
subconjuntosen el caso base? ¡Esta es una parte difícil de hacer bien! - ¿Cuántos subconjuntos de {Pretzel, Manzana, Naranja, Banana} contienen Pretzel? ¿Cuántos no?
- Describa "los subconjuntos de {Pretzel, Manzana, Naranja, Banana} que no contienen Pretzel" sin usar las palabras "no contienen".
-
Esta es una versión de cómo se vería el código, con muchos espacios para llenar…