- Write down all the subsets of {Apple, Orange, Banana}. How many are there?
- Write down all the subsets of {Pretzel, Apple, Orange, Banana}. Try to do this with as little work as possible.
Add a question that gets at how 2 is just an augmentation of 1. --MF, 6/17/20
 Describe how you did it.
Describe how you did it. -
MARY Note to self: this is hard. for example, in base case (subsets of empty list), you have to report a list containing the empty list. Add a question that gets at the base case.Now create a
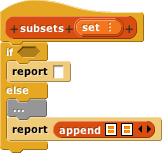
subsetsblock that takes a list as input and reports a list of lists in which each item is a subset of the original input list. The order in which the subsets appear in the output list doesn't matter, but each subset must appear exactly once. The result might look like this:

If you're stuck after trying as many ideas as you can think of, click here for some help.
- How many subsets does the empty set {} have?
- What should
subsetsreport in the base case? This is a hard part to get right! - How many subsets of {Pretzel, Apple, Orange, Banana} contain Pretzel? How many don't?
- Describe "the subsets of {Pretzel, Apple, Orange, Banana} that don't contain Pretzel" without using the words "don't contain."
-
Here's one version of what the code might look like, with many spaces to fill…