- Write out Row 7 of Pascal's Triangle.
-
Write a
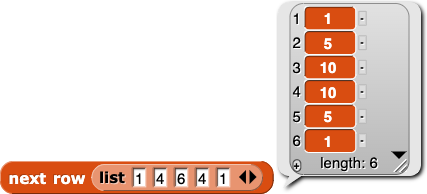
next rowblock that takes a row of Pascal's Triangle as its input, and reports the next row as its output:
PG: These are projects and should be listed as projects. Nice enough suggestions, but optional. And why are "simple ones" after all the (implicitly and, I think, really) hard stuff? It would be great to have a collection of puzzles, like the ones Parisa hands out, for kids to sink their teeth into, but /they/ already knew how to program recursively. I don't think we've provided what is needed for our kids to master that.
MF: I want to review/revise.
In Pascal's Triangle, each number is the sum of the two numbers above it. The numbers at the ends of each row are always 1.
Row 1: 1 1
Row 2: 1 2 1
Row 3: 1 3 3 1
Row 4: 1 4 6 4 1
Row 5: 1 5 10 10 5 1
Row 6: 1 6 15 20 15 6 1
︙
For example, each 15 in Row 6 is the sum of the 5 and 10 just above it.
next row block that takes a row of Pascal's Triangle as its input, and reports the next row as its output:
To refer to a specific number in Pascal's Triangle, you need to know its row and column. Rows are simple; columns are more complicated because of the triangle's orientation. Here is Pascal's Triangle, aligned in columns:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Pascal's Triangle counts the number of ways to pick a collection from larger collection. For more about Pascal's Triangle and its uses, see About Pascal's Triangle page.
pascal block that takes two numbers as input, row and column, and reports the value in that row and column of Pascal's Triangle.