pascal: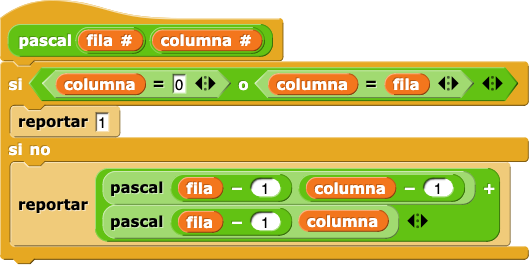
Aquí hay una solución para el bloque pascal:

Hay dos casos base, el principio y el final de una fila. El caso recursivo calcula la suma de dos valores en la fila anterior.
 =
=  +
+ 
Estás a punto de averiguar cuántas llamadas recursivas se necesitan para calcular un valor en el triángulo de Pascal.
pascal para llevar la cuenta de cuántas veces se ejecuta el bloque.pascal al calcular  ?
? ?
? para ver la redundancia.
para ver la redundancia.Muchas de las llamadas recursivas son redundantes. Por ejemplo:  llamará a
llamará a  muchas veces, pidiendo la misma información.
muchas veces, pidiendo la misma información.
pascal, de modo que, cuando se vuelvan a proporcionar las mismas entradas, la función busque el valor guardado en lugar de realizar más llamadas recursivas.pascal que se usa mucho:
Crea una versión de pascal que use la fórmula. Compara la eficiencia de esta versión con la versión recursiva y determina si cada versión se ejecuta en tiempo constante, tiempo lineal, tiempo cuadrático o tiempo exponencial.