Pascal's Triangle and Efficiency

BH an MF: block should be renamed pascals triangle, row: () position: () in the style used throughout the rest of the course. --MF, 4/1/19

PG: Efficiency is important, even in the AP framework (though that's irrelevant at this time of year) but is a distraction until kids are so fluent with recursion that they're able to think about efficiency.

BH: End of lab 3

MF: I want to review/revise.

Pages or lab needs renaming so they aren't duplicative. --MF, 6/15/20

Here's one solution to the pascal block:

Image needs to be rebuilt. --MF, 4/22/22
pascal(row)(column){if(column=0 or column=row){report(1)} else{report(pascal(row-1)(column-1) + pascal(row-1)(column))}}

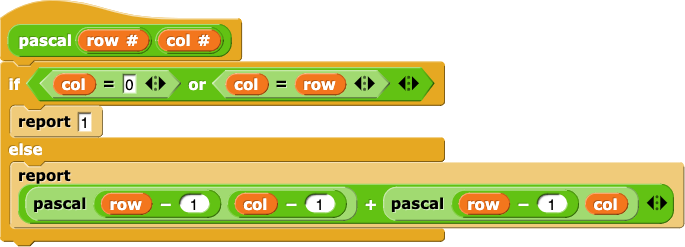
There are two base cases, the beginning and end of a row. The recursive case calculates the sum of two values in the previous row.

pascal(14)(5) = pascal(13)(4) + pascal(13)(5)

You are about to figure out how many recursive calls are needed to compute a value in Pascal's Triangle.

What could you insert inside the block to track this?
  1. Modify your pascal block to keep count of how many times the block is executed.
  2. How many times is the pascal block called when calculating pascal(14)(5)?
  3. What happens when you call pascal(20)(5)?

Many of the recursive calls are redundant. For example, pascal(14)(5) will call pascal(10)(3) many times, asking for the same information.

Track what pascal(14)(5) actually calls to see the redundancy.
This technique is called memoization. This is not a typo; there's no "r" in the word. Each recorded answer is like a "memo".
  1. Use a list structure to keep track of already-computed values of pascal, so that when the same inputs are given again, the function looks up the saved value instead of making more recursive calls.
  2. There is a direct formula for pascal that is often used:
    \text{pascal}(n,r) = \frac{n!}{r!(n-r)!}
    PG: I'm ignoring for the moment the fact that I'm not sure we've taught enough about "quadratic time" etc. for the kids to tell.

    Build a version of pascal that uses the formula. Compare the efficiency of this version to the recursive version, and determine whether each version runs in constant time, linear time, quadratic time, or exponential time.