5.1.2: Problem and Instance of a Problem  

• A problem is a general description of a task that may (or may not) be solved algorithmically.
• An instance of a problem is one case of a problem, with specific inputs.

5.1.2: Linear Search or Sequential Search  

• An algorithm takes linear time if multiplying the input size by ten multiplies the time required by ten.
  
AAP-2.O.5
• A linear search (or sequential search) algorithm checks each element of a list in order, a process which takes linear time.

5.1.3: Binary Search  

A binary search algorithm starts in the middle of a sorted list and repeatedly eliminates half the list until either the desired value is found or all elements have been eliminated.

Linear search does a complete traversal of the list. Binary search saves time by doing a partial traversal of the list.

5.1.4  

The relationship between the input size and the number of steps required to solve a problem is the efficiency of the algorithm used to solve the problem.

5.1.5  

• An algorithm takes linear time the number of steps is proportional to the input size; doubling the input size doubles the time required.
• An algorithm takes sublinear time if the number of steps grows more slowly than the size.
• An algorithm takes constant time if it takes the same number of steps regardless of input size.
• An algorithm takes quadratic time if the number of steps is proportional to the square of the input size.

5.1.5  

• An algorithm takes polynomial time if the number of steps is less than or equal to a power of the size of the input, such as constant (n⁰), sublinear, linear (n¹), quadratic (n²), or cubic (n³).
• An algorithm takes exponential time if the number of steps is proportional to an exponential function of the size of the input, such as 2ⁿ, 10ⁿ, etc., which is much slower than any polynomial.

5.1.6  

• A decision problem is a problem with a true/false answer (for example, "is 5,825,496,221 a prime number?").
• An optimization problem is one with the goal of finding the best solution among many (for example, "what's the best school schedule to place every student into as many of their requested classes as possible?").

5.1.6  

A decidable problem a decision problem for which it's possible to write an algorithm that will give a correct output for all inputs.

An undecidable problem is the opposite. It's not possible to write an algorithm that will give a correct output for all inputs—even though it might be possible for some of them.

5.1.8: Sequential and Parallel Computing  

This section covers two computational models:

• In sequential computing, operations are performed in order one at a time.
• In parallel computing, the program is broken into smaller steps, some of which are performed at the same time. Modern computers have multiple processors (2, 4, or 8) in a single computer, so you can do small-scale parallel processing on the machine on your desk.

5.1.8  

Distributed computing is a form of parallel computing that uses multiple computers (perhaps even spread out around the world).

5.1.8  

A processor is a piece of circuitry inside a computer that processes the instructions from computer programs.

Image credit: Wikipedia user Solipsist

5.1.8  

Programmers refer to the speedup of parallel solution to describe how many times as fast the parallel solution is compared to the sequential solution:
\text{speedup} = \frac{\text{sequential time}}{\text{parallel time}}

5.2.1  

Simulations are computer representations of real things or situations that vary over time. A simulation is an abstraction designed for a particular purpose.

5.3.1: Data vs. Information  

• Data are the values that computers receive from various sources, including human activity, sensors, etc.
• Information is the humanly-useful patterns extracted from data.

Data provide opportunities for identifying trends, making connections, and addressing problems. Information is the result of analyzing that data.

5.3.1  

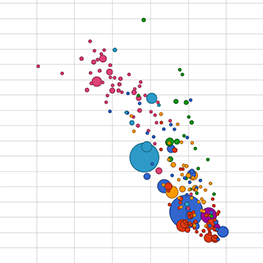
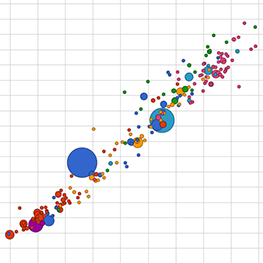
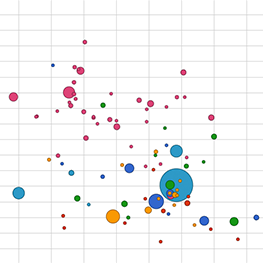
A correlation is a particular kind of information, namely a dependence between two variables. For example in the first picture here, as one variable goes up the other goes down. It's also a correlation when as one variable goes up or down the other changes in the same manner.

5.3.1  

Insight is a meaningful conclusion drawn from analyzing information.

5.3.3: Records, Fields, and Columns  

• A record is one row in a dataset (other than the first row, which contains the column headings). A single record might be the data for one student in your school, the data for one earthquake that happened, the data for one hospital in the U.S, or the data for one contact in your contact list. In other words, a record is a horizontal slice of the dataset.
• A field is one item of a record in a dataset. It might be one person's homeroom teacher, the magnitude of an earthquake in Los Angeles last week, the owner of one hospital in Chicago, or the phone number of one person in your contact list.
• A column is a list containing the data from one field for all records in a dataset. A column might be the homeroom teacher for every student in your school, the magnitude of every earthquake in the dataset, the owner of every hospital in the U.S., or the phone number of every person in your contact list. In other words, a column is a vertical slice of the dataset.

5.3.3  

Cleaning data is the process of making the data uniform without changing its meaning (such as replacing abbreviations, spellings, and capitalizations with the intended word or converting miles to kilometers). Programmers can use programs to filter and clean digital data, thereby gaining insight and knowledge.

5.3.5  

Classifying data means distributing data into groups based on common characteristics.

5.3.5   The mode of a data set is the value that appears most often in it.

5.3.6  

Metadata are data about data. For example, the piece of data may be an image, while the metadata may include the date of creation or the file size of the image.

5.4.1  

A proof by contradiction is a two-step proof that a statement is false, which is done by:

1. assuming the statement is true
2. based on that assumption, proving something known to be false (that is, showing the assumption creates a contradiction)

5.4.1  

An undecidable statement might be true or might be false; we don't know which.

A self-contradictory statement can be neither true nor false.

5.4.2  

An infinite loop is a sequence of computer instructions that repeats forever.

An unsolvable problem is one for which no algorithm can ever be written to find the solution.

An undecidable problem is one for which no algorithm can ever be written that will always give a correct true/false decision for every input value. Undecidable problems are a subcategory of unsolvable problems that include only problems that should have a yes/no answer (such as: does my code have a bug?).