Unit 3 Lab 1 Teacher Guide

• 25–50 minutes (about 1 class period) on Robot in a Maze
• 15–30 minutes (<1 class period) on Fractal Art
• 10–20 minutes (<1 class period) on Using Abstraction to Nest Triangles
• 20–40 minutes (<1 class period) on Brick Wall
• 30–60 minutes (about 1 class period) on Building a Tic-Tac-Toe Board
• 10–20 minutes (<1 class period) on Debugging Recap

• Page 1: Robot in a Maze.
  • Learning Goals:
    • Gain experience with a type of question (robot movement) that often appears in AP CSP exams.
    • Satisfy AP CSP Framework items requiring students to develop algorithms without coding them. Following a maze is a nontrivial problem.
  • Tips:
    • The AP CSP Framework talks in several places about sequence, selection, and repetition as the building blocks of an algorithm. This triad of building blocks comes from a piece of theoretical computer science called the Structured Program Theorem (Wikipedia), which proves that any algorithm can be expressed using those building blocks. The historical importance of this theorem was that at the time (1966) most programming included "go to" statements that would jump into the middle of loops, or just anywhere, resulting in "spaghetti code" that was hard to debug. But the theorem was a theoretical minimum structure, like a Turing Machine, not meant as a practical programming discipline. Instead, the Structured Programming discipline based on it includes a fourth, extremely important control structure: the procedure call. As you know, this is the basis of most forms of abstraction, the most central idea in computer science. Indeed, a different minimum structure theorem, due to Alonzo Church, proved (decades earlier) that any algorithm can be encoded in Lambda Calculus, using nothing but the ability to create a procedure and the ability to call a procedure. You don't even need any naming mechanism (such as assignment to variables) other than procedure inputs. Nobody really programs in such a stripped-down language (you don't even get arithmetic!), but it's useful for proving theorems about what computers can and can't do. Since modern programming languages don't even have a "go to" statement, the CSP Framework is fighting a battle that was over 50 years ago. Nevertheless, we humor them, but we also try to teach students that procedures are at least as important as the other three.
    • "Follow the left wall" seems to fail in the maze on this page, because it gets you back to the starting point. But keep going, still touching the left wall, and it will eventually get you to the exit.
• Page 2: Fractal Art.
  • Learning Goals:
    • Understand the result of nested repeat blocks.
    • Read a program and predict the result of running it.
  • Tips:
    • On this page we tell students to duplicate (copy and paste) a block of code, so that they can insert the copy into the original. Students who are on the ball may remember that back on U1L2p2 we told them not to copy and paste code, but instead to put the code in a custom block, and call that block in both places. If so, congratulate them on paying attention, and tell them that we're going to fix the problem on the next page.
    • If students wonder about the 120° turn in the triangle, have them review U1L3 on drawing polygons.
• Page 3: Using Abstraction to Nest Triangles.
  • Learning Goals:
    • Explore recursion, one of the greatest ideas in computer science.
  • Tips:
    • Mathematics Note: Preview of recursion. The figures in the animation at the top of the page seem quite complicated. But they can be generated by a programming style that previews a technique that will be developed in more depth in Unit 6. To get a feel for what's going on, start with a script that draws a triangle:
      
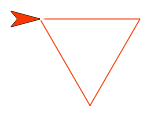
      Now make it take a break at each vertex and do something simple, like play a note:
      
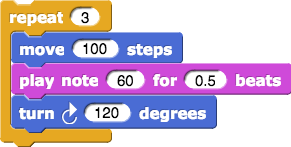
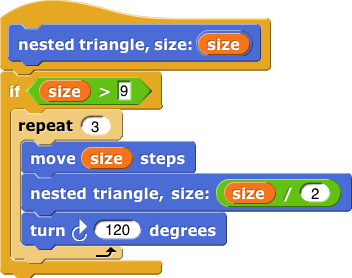
      Instead of making it play a note, have it draw a smaller triangle:
      
      Now you can get as intricate as you want by inserting ever-smaller triangles between each move and turn.
    • Recursion is one the most profound (and potentially difficult) concepts in all of computer science due to its self-referential nature. Your kids (and you) will succeed now, but comfort and mastery can take a long time. This is just an appetizer; with more experience later this year, the purpose and enormous value of recursion will become more apparent.
    • If you had exposure to recursion before, you may be wondering where in our code we are dealing with the "base case" that terminates the iterative process. A little reflection will show that the condition that terminates the recursion is the if (size > 9) block and the implicit "base case" is: if size ≤ 9 then stop drawing.
      
• Page 4: Brick Wall.
  • Learning Goals:
    • Get more experience with abstraction in the context of developing blocks that specialize on specific tasks.
    • Use abstraction to create a somewhat complex program built on relatively simple custom blocks.
    • Learn the programming strategy of getting individual aspects working completely instead of trying to build all aspects simultaneously.
  • Tips:
    • Note three levels of procedural abstraction: a wall is made of rows, which are made of bricks, which are made out of primitive move blocks.
    • Most students will find it easier to develop the draw row A block than the draw row B block due to its two smaller bricks. Getting the two rows to span the same length will require some trial and error.
    • The draw brick wall block definition must identify whether an even or an odd numbered row is being built. One way to do that is to call odd? on the row number for each row. Another way is to make height/2 repetitions of a draw row A and a draw row B, then see if the total height is even or odd to decide whether or not to draw a final draw row A.
    • Encourage students to think about what helper blocks besides draw brick they might want.
    • Ten minutes before the end of class, make sure that students discuss the question: "How do you think procedural abstraction manages the complexity of a program?" Take reports from several groups and collectively converge on a single explanation.

    Too much abstraction? It's possible to go overboard on abstraction and build so many blocks that your program is just as cluttered as it would be without the special blocks.

    But it can also be useful to make a special block even when its definition is just one built-in block. For example, to draw the mortar (the cement between bricks, shown as white space), you can just use move (4) steps, but it might make sense to define a draw mortar block.

    Why? You might later decide that 4 steps is the wrong thickness for mortar, and you'd rather have 5. Or you might want the mortar to be cement-colored, slightly gray. With many move blocks scattered through your program, you would have to find and change each one, and keep putting in set pen color blocks. With a draw mortar block, you can just change its definition and all the mortar in your picture will be changed.

• Page 5: Building a Tic-Tac-Toe Board.
  • Learning Goals:
    • Appreciate the important CS concept of parallelism—the fact that multiple processes can be running at the same time (in this case, multiple sprites remaining simultaneously "aware" and waiting for a click).
  • Tips:
    • Later when students extend Tic-Tac-Toe to check for legal moves, to check for wins, and ultimately to have the machine play competently, the machine will need to keep a record of each move. The approach in previous years to Tic-Tac-Toe required the programmer to design a way to sense where on the screen a player moved; in this alternative version, the squares of the Tic-Tac-Toe board are click-conscious sprites, thus eliminating the need for the programmer to compute the board cell numbers from the coordinates of the mouse click. This approach takes advantage of a capability of Snap! that is not in all programming languages—clones—a sophisticated and valuable abstraction that simplifies the programmer's task in languages that provide it.
    • This project hints at two important modern ideas in computer science:
      • One is object oriented programming: Instead of a single sequence of instructions, the program has several independent objects (also called "agents" or "actors"), each of which has its own behavior. In this project, the player can only click on one sprite at a time, and it then carries out a very quick task (changing costume) before the player clicks another sprite. But a more complicated program might have one sprite send a message to another sprite, which would respond with its own behavior, while the first sprite continues with its own script.
      • The other idea is parallelism or distributed computing. This project runs on a single computer, and the apparent ability of sprites to run simultaneously is an illusion provided by Snap!, which runs one script for a little while, then switches to a different script, and so on, then updates the display, then continues the first script. But it's possible to use nine separate computers, one for each sprite. That would be overkill for this small project, but large web servers such as Google or Twitter have many thousands of computers all cooperating to handle the large amounts of data they require.
• Page 6: Debugging Recap.
  • Learning Goals:
    • Review previously learned strategies for debugging and preventing bugs.
  • Tips:
    • Some of these suggestions and strategies might make for a nice classroom poster.

• Abstraction: Abstraction & Detail Removal
• Abstraction: Generalization
• Abstraction: Abstraction Interfaces and Summary
• Abstraction: Power, Limitations

The Unit 3 Assessments and Solutions are available only to teachers. For access, please sign up here.