getBinaryDigits with this method we get: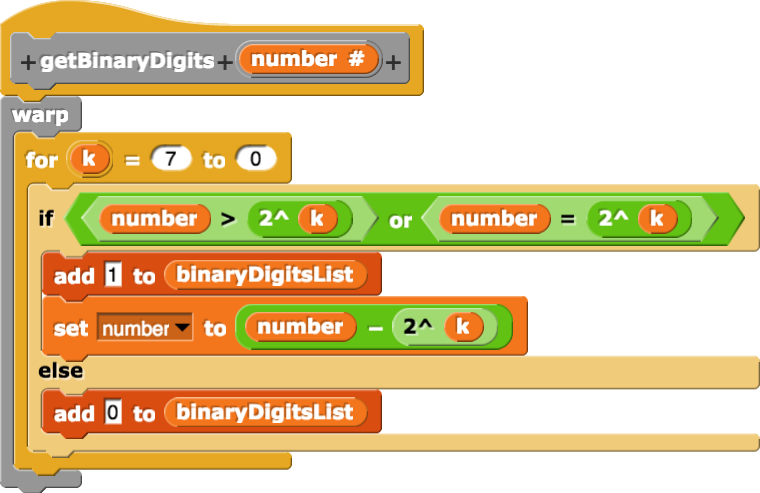
If you study the examples presented here, you will notice that method 2 (Descending Powers of Two and Subtraction) is easier to understand and code so it is recommended that you try this first. The algorithm goes something like this:
Starting with the largest power of 2 down to the lowest power of 2 (in our case from 27 to 20 as there are 8 binary digits) check if that power of 2 is contained in the number (i.e. if the number is greater than or equal to that power of 2.) If so, write 1 for the current binary digit and replace the number with that power of 2 subtracted from the number. Otherwise, write 0 for the current binary digit.
Implementing getBinaryDigits with this method we get:

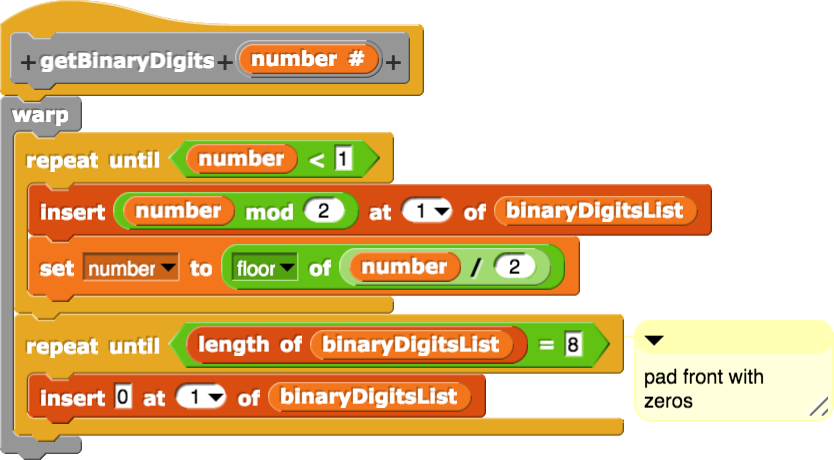
If you decide to code getBinaryDigits with method 1 (Short Division by Two with Remainder), then you will need to compute a lot of remainders and quotients during division with 2, which you can get by using the mod and floor operators respectively in Snap!. The code may look like this. Notice how similar it is to the getDecimalDigits code.