En esta página, realizarás iteraciones para repetir y contar las repeticiones con el objetivo de usar un contador para dibujar formas con patrones repetidos.
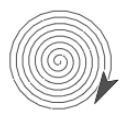
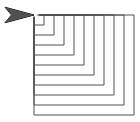
En esta página, realizarás iteraciones para repetir y contar las repeticiones con el objetivo de usar un contador para dibujar formas con patrones repetidos.


Ya conoces las siguientes formas de repetir un grupo de comandos:
por siempre genera un ciclo infinito que funciona por siempre. Un ciclo infinito puede ser a veces el resultado de un error, aunque en algunos programas interactivos se desea que el programa se mantenga ejecutándose hasta que es detenido por el usuario. repite los bloques que se encuentran en su interior por siempre. (Se usó este bloque para hacer que Alonzo se mantuviera moviéndose en el laboratorio Unidad 1 Laboratorio 1 Página 3: Programar un juego)
repite los bloques que se encuentran en su interior por siempre. (Se usó este bloque para hacer que Alonzo se mantuviera moviéndose en el laboratorio Unidad 1 Laboratorio 1 Página 3: Programar un juego) repite los bloques en su interior un número específico de veces. (Se usó este bloque para dibujar formas en el laboratorio Unidad 1 Laboratorio 3 Página 1: Explorar el movimiento)
repite los bloques en su interior un número específico de veces. (Se usó este bloque para dibujar formas en el laboratorio Unidad 1 Laboratorio 3 Página 1: Explorar el movimiento)Los científicos de la computación definen una estructura de programa repetitivo como un ciclo, repetición, o iteración (iteration).
El código puede repetirse por siempre, un número específico de veces (al usar repetir) o bien hasta que una condición específica se cumpla (por ejemplo al usar repetir hasta que, como se presentará en el Laboratorio 5).
.es.png)

Algunas veces el código dentro de un ciclo necesita saber en qué iteración se encuentra (primera, segunda, etc.).
Se puede usar el bloque  para llevar el control, y se puede usar su contador en el código a repetir (está representado por defecto por la letra "i"
para llevar el control, y se puede usar su contador en el código a repetir (está representado por defecto por la letra "i"  ). Por ejemplo, el bloque
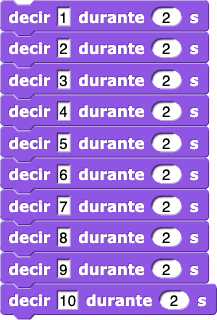
). Por ejemplo, el bloque para brinda la oportunidad de simplificar un código largo como el siguiente:
 en
en

Cada vez que el bloque para ejecuta el código en su interior, incrementa el valor del contador en 1, empezando con el primer valor y terminando en el último valor que aparece (en el ejemplo el 10).
para define con i (letra i significa "índice") el nombre de contador de forma predeterminada. Puedes cambiar el nombre haciendo clic sobre él. Para usar el contador, arrástralo a la ubicación requerida.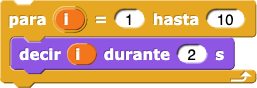
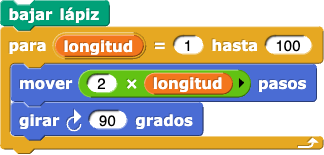
para en el código anterior. ¿Cuál es el resultado?girar y mover para obtener un resultado más parecido a un espiral normal similar a:
cuadrados anidados que haga uso de los bloques para y polígono para dibujar cuadrados anidados. Proporciona un valor de entrada que dibuje número de cuadrados a especificar, con cada cuadrado más grande que el anterior: 
polígonos anidados que reciba el campo de entrada número de polígonos y número de lados para los polígonos a dibujar.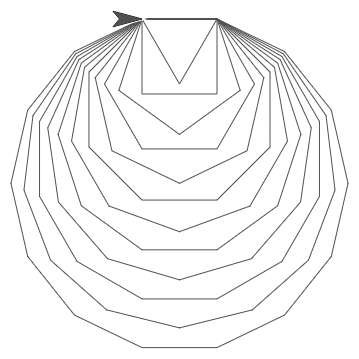
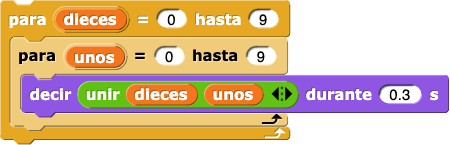
molinete con campos de entrada. Encuentra la forma de crear tus propias animaciones artísticas.

El código que se presenta a continuación puede darte la idea de cómo crear animaciones. El bloque unificar permite dibujar el molinete de inmediato.
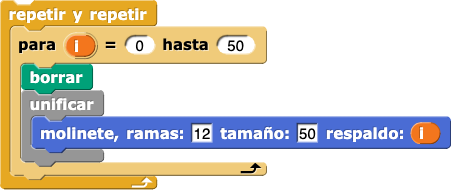
 Asegúrate de guardar tu otro trabajo, luego
Asegúrate de guardar tu otro trabajo, luego 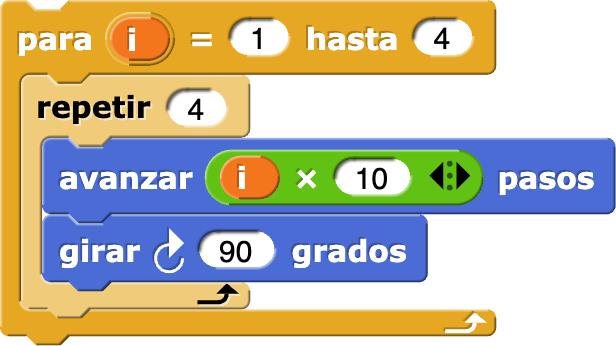

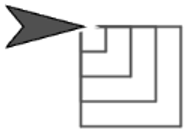

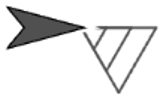
para con el objetivo de enlazar cuadrados de la forma que se presenta en las imágenes. Construye un bloque con dos campos de entrada que permitan especificar la cantidad de cuadrados que contendrá la pintura y qué tan grande será el cuadrado actual en relación al anterior.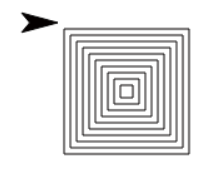

A la derecha se muestra una pintura de Josef Albers. A este pintor le interesaba experimentar con una variación de colores dentro de una "familia" de colores similares. Snap! permite hacer experimentos similares.
 entonces debes leerla ahora
para aprender las funcionalidades de Snap! para rectángulos sólidos y familia de colores.
entonces debes leerla ahora
para aprender las funcionalidades de Snap! para rectángulos sólidos y familia de colores.mover, cambia el valor de girar: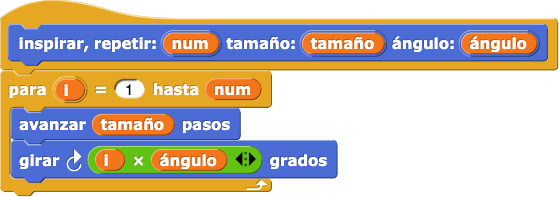
 Es útil si estás seguro que no pasará nada nuevo, ¡pero no lo decidas tan rápido!
Es útil si estás seguro que no pasará nada nuevo, ¡pero no lo decidas tan rápido!