Unit 5 Lab 1 Teacher Guide

In a reversal of their Unit 2 number guessing game, students design an algorithm that identifies the player's secret number by: guessing, asking the player if the guesses are too high or too low, and guessing again until guessing right. Students use this as a basis for developing and analyzing list searching algorithms for ordered and unordered lists.

An efficient list searching algorithm depends on the fact that numbers have order. Searching an ordered list to find the location of a given object is most efficiently done with essentially the same algorithm. Searching for the location of an object in an unordered list cannot be done the same way. The time that it takes these two algorithms to find their objects hardly matters when the lists are small, but matters a lot when the lists get large. This is students' first experience analyzing computational complexity.

Pacing:

Lab Pages

Brian, I suggest using some of this to fill in the blanks in the TG below... --MF, 11/17/19

Page 1: Searching a Sorted List.

Learning Goals:
- Invent a strategy for reliably guessing a number.
- Implement an algorithm for reliably guessing a number.
Prepare: Day 2—Off-Computer Game.
- Decide how to split your class into small groups with two teams each.
- Prepare materials for each group: 15 paper cups numbered 1 through 15 and 25 small cards numbered 1 through 25, which fit inside the cups.
Tips:
- Begin with student lab page. As you circulate, ask about students' strategies for number guessing and their programming ideas. If there is time, you may want to ask various students to share strategies.
- If students don't yet come up with a clear understanding of the algorithm, the following cups game gives them yet another chance.
- Start the second day with this off-computer game, then use remainder of period to complete first lab page:
  - Setup:
    - Assign teams and hand out materials described in Prepare section above.
    - Explain the game, and pose or post the "Questions to consider during play" (below).
    - Team 1 secretly arranges the cups in numerical order with exactly one card in each cup. Cards will be left over, but the ones in the cups must be in numerical order.
    - Team 2 selects a number at random, using , and tells Team 1.
  - Goal: Team 2 tries to figure out, using the fewest questions, which cup that number is in or whether that number is not in any cup.
    - Team 2 players may ask only "Is it in cup number ____?"
    - Team 1 may answer only "yes" or "the number in that cup is higher/lower than the number you are looking for."
  - Questions to consider during play:
    - What strategies can help you find a particular number with the fewest location checks?
    - On average, how many guesses would it take to find a number?
    - How many guesses would it take to determine that a number didn't exist in the list at all?
    - How much more work would it be to find a number if the number of cups were doubled?
  - Discussion after game:
    - Have students share some of their thinking about the four questions above.

Page 2: Analyzing and Improving Searches.

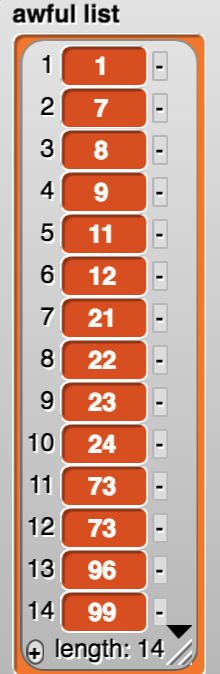
Brian, if you keep these images, please don't call it "awful list." How about "sorted list" or something else that's appropriately descriptive? --MF, 11/17/19

awful list {1, 7, 8, 9, 11, 12, 21, 22, 23, 24, 73, 73, 96, 99}

Learning Goals:
- Implement an algorithm for searching unsorted lists.
- Consider how the size of the search territory influences the amount of time that the search takes.
- Modify the number guessing algorithm for searching sorted lists.
- Implement an algorithm for searching sorted lists.
Discussion: After students work through the lab page, you might ask: "Which takes fewer computer steps, finding a number in a sorted list or finding a number in an unsorted list?"
Tips:
- Introduce programming activity by saying that the first part of the lab asks you to figure out a strategy for finding a number if the list is not sorted.
- You might want to connect searching a sorted list with mean, median, midrange. In this list, 50 is the midrange, exactly midway between 1 and 99, but is a poor place to start the search because it doesn't split the list in half. The mean is approximately 34, which is no better. What we are looking for is the median, the number in the middle of the sorted list. Students may find it helpful to define blocks that find the mean and median of lists of numbers.

Page 3: List Processing Algorithms.

Learning Goals:
- Use a recursive algorithm to develop code for checking if the elements of a list are distinct.
- Use this code to develop code for reporting the duplicate items in a list.
Tips:
- Students may have different impressions of the pseudocode steps as written. Encourage them to rewrite it in their own words. The concept here is to give students a clearer picture of ways they can organize their work somewhere in between a written language and their code.
- In particular here, if a student misunderstands some of the pseudocode, get another student to help them with an alternate description. Or try to get the student to write something more useful to them. Ideally, don't show them the corresponding code, as this shortcuts the activity.
- There are multiple ways to make the list of duplicates. Expect most students to build an algorithm similar to the one that determines if the unique list exists. If time permits and you see different algorithms used, highlight their differences. You can also use these algorithms in later labs as your examples for timing tests.

Page 1: Guess My Number.
- Learning Goals:
  - Students invent the binary search algorithm by observing their own guesses and trying to improve their play.
  - They then implement the algorithm for the computer to use while guessing.
- Tips:
  - Students have built the version of the game in which the human player does the guessing in Unit 2. Some will already have discovered the binary search algorithm. Indeed, some may have played the game in elementary school math class.
  - When students implement the program that lets the computer guess the human player's number, there is no scaffolding at all for the programming. We're in Unit 5, almost ready for the AP exam, and they need to have some skill at coding by now. Reassure them (and yourself) that they can do this, and refrain from giving them code. Instead, tell them to read the algorithm description they've just written.
  - By the way, they wrote the algorithm in English in the context of teaching it to another student. This is a much more natural and honest context for writing algorithms in text than talk of "pseudocode"; if you're writing an algorithm for a computer to use, the only reason not to write it directly in code is that you're using a bad programming language. But other human beings are "programmed" in English.
Page 2: How Many Five-Letter Words Are There?
- Learning Goals:
  - Students will use the computation time of block to measure the running time of a process.
  - Students will understand what it means for a process to take linear time: The time is proportional to the size of the input.
- Tips:
  - As the page reminds them, students have already written the (one-line) function, using keep, to count the number of five-letter words. If they've forgotten, let them review the linked page.
  - It's important that they do problem 5 (estimate the time for a ten-times-as-long dictionary) before problem 6 (do the experiment).
  - Note that the inner green box invites students to look inside the computation time of block. It's a simple piece of code, won't take long to read, and may be useful in demystifying the measurement of time.
  - The block measures "wall clock time": the actual elapsed time, not the amount of time the computer actually spends running this program. Modern operating systems start roughly 100 programs when they are booted; all those programs compete with Snap! for computer time. That's why running the same experiment twice will generally give different answers.
  - Don't obsess over the difference between a problem and an instance of the problem, but there is a reason for making the distinction: An instance of the problem, working with specific inputs, takes constant time! (Maybe a small constant, maybe a large constant, but either way it's constant.) It's only when you compare several instances of the problem that you can observe how running time varies as a function of problem size.
  - Keep is a Snap! primitive, but that doesn't mean it takes constant time. Most primitives do take constant time (think about arithmetic operators, sprite motion, and so on), so some students may assume that all primitives are constant time. But even not counting higher-order functions, the contains predicate for lists takes linear time.
  - Don't neglect problem 7. It's not always obvious which of several sizes in a problem is the relevant one for timing computations.
Page 3: Is "Seperate" Spelled Correctly?
- Learning Goals:
  - The goal of this page is for students to understand and time binary search.
- Tips:
  - The main difference between guess my number and binary search is that in the former, each number is its own position. (That is, in the numbers from 1 to 10, 3 is the third number.) So there's no need to consider the position and the value at that position separately. But in binary search of a dictionary, after computing the middle position in the list, you have to actually retrieve that item of the list with the item block.
  - Don't bring this up unless a student asks, but the comparison predicates, when applied to numbers, don't compare alphabetically; 2 comes before 12 as a number, even though in alphabetical order, "2" would be compared with the first digit of "12," i.e., with "1."
  - Don't bring this up, either, but if you do a binary search of a linked list (one that was constructed with the in front of function rather than by mutation) it'll take somewhat more than linear time, because each call to item takes linear time instead of constant time. It won't happen with the dictionaries in the starter project.
  - The "If There Is Time" project, a spell checker, is fun and useful.
Page 4: Exactly How Much Faster Is Binary Search?
- Learning Goals:
  - Students will determine that binary search takes less than linear time, both by experimental measurement and by counting the number of constant-time steps required.
- Tips:
  - After students have they've made their tables, have a few students share their times and observe the variation. Then have a few students share their number of steps and observe that everyone (ideally) has the same count for the steps. This is because the number of steps is a fixed quantity, whereas the time the algorithm takes to run depends on the speed of the computer and what else it's doing at that moment.
  - Students may notice that there are actually two comparisons in every iteration for binary search: an = and a <. We are considering that to be just one step, but if they want to count each as its own step, that's fine; they will just get twice as many steps for each list in their table.
  - If your students are old enough to have studied logarithms, you can ask them to determine the exact number of comparisons needed as a function of the list size, namely f(n)=⌈log₂n⌉. (Of course this is a worst case time; you might be lucky enough to be searching for the word exactly halfway through the list.) But if they haven't studied logs, it's not important; they should just see how dramatically lower the number of guesses is than the size of the list.
Page 5: Categorizing Algorithms.
- Learning Goals:
  - Understand examples of constant time, sublinear (e.g., log) time, linear time, quadratic time, and exponential time.
- Tips:
  - Because 25,000 is a big number, students may find it counterintuitive that it's in the fastest category (constant time). But this is a case in which the relevant number is, indeed, 25,000—but it's always 25,000. 25,000 numbers starting at 1,000,000 takes just as long as 25,000 numbers starting at 1. So the input to the function is irrelevant.
  - We provide a sort function that takes quadratic time, not the most efficient possible, because we want students to understand quadratic time. Optimal sort algorithms take n log n time.
  - The exponential-time algorithm, the one that finds values in Pascal's triangle by adding the two values above the one you want, is in an If There Is Time. But try to fit this in; the experience of measuring an exponential-time function will really give students an intuitive feel for how unreasonable an exponential-time algorithm is. Just reading about it isn't the same.
Page 6: Heuristic Solutions.
- Learning Goals:
  - Students will learn that some exponential-time problems have faster approximate or good enough solutions.
- Tips:
  - We are not asking students to write a real example of a heuristic solution. So this page is entirely offline discussions or even lecture if you must.
  - The "can all decision problems be solved" part of the page introduces the topic of Lab 4: undecidable problems. It's here because the College Board only expects students to accept on faith that there are such problems, so some teachers decide to skip Lab 4, in which we prove it.
Page 7: Removing Duplicates.
- Learning Goals:
  - Distinct items is another example of a quadratic time algorithm.
  - Students are guided to a recursive solution, introducing them to recursions on lists.
- Tips:
  - Expect some students to have trouble understanding the base case of the predicate version they write first. Are the items of an empty list distinct? There aren't any items, so students will be tempted to report False. But the right way to think about it is that there aren't any non-distinct items, so all the (nonexistent) items are indeed distinct.
  - This algorithm takes quadratic time. If you have some students who are way ahead of the class, tell them that a good rule of thumb is to see if sorting the data (with an n log n algorithm like the one in the "list utilities" library, not the n² one in this lab's starter project) will allow a solution in less than quadratic time. And in this case it will, because each item has to be compared only to the one just after it, rather than to all the others.
Page 8: Parallelism.
- Learning Goals:
  - Many problems can be solved more quickly with parallelism.
  - Even home computers these days have a small degree of parallel capability.
  - For several reasons, using n processors instead of one doesn't divide the runtime by n.
  - Writing software to benefit from parallelism is hard to get right.
- Tips:
  - In the examples using wait blocks, it's important to notice the "and wait" in the broadcast block that starts the parallel scripts; that's what makes the wait in the same script happen after the parallel threads have finished.

Solutions

Correlation with 2020 AP CS Principles Framework

Computational Thinking Practices: Skills

1.A: Investigate the situation, context or task.
1.D: Evaluate solution options.

Learning Objectives:

AAP-2.P: For binary search algorithms:
- Determine the number of iterations required to find a value in a data set. (1.D)
- Explain the requirements necessary to complete a binary search. (1.A)
AAP-4.A: For determining the efficiency of an algorithm:
- Explain the difference between algorithms that run in reasonable time and those that do not. (1.D)
- Identify situations where a heuristic solution may be more appropriate. (1.D)
AAP-4.B: Explain the existence of undecidable problems in computer science. (1.A)
CSN-2.A: For sequential, parallel, and distributed computing:
- Compare problem solutions. (1.D)
- Determine the efficiency of solutions. (1.D)
CSN-2.B: Describe benefits and challenges of parallel and distributed computing. (1.D)

Essential Knowledge:

AAP-2.O.1: Traversing a list can be a complete traversal, where all elements in the list are accessed, or a partial traversal, where only a portion of elements are accessed.
AAP-2.O.5: Linear search or sequential search algorithms check each element of a list, in order, until the desired value is found or all elements in the list have been checked.
AAP-2.P.1: The binary search algorithm starts at the middle of a sorted data set of numbers and eliminates half of the data; this process repeats until the desired value is found or all elements have been eliminated.
AAP-2.P.2: Data must be in sorted order to use the binary search algorithm.
AAP-2.P.3: Binary search is often more efficient than sequential/linear search when applied to sorted data.
AAP-4.A.1: A problem is a general description of a task that can (or cannot) be solved algorithmically. An instance of a problem also includes specific input. For example, sorting is a problem; sorting the list (2,3,1,7) is an instance of the problem.
AAP-4.A.2: A decision problem is a problem with a yes/no answer (e.g., is there a path from A to B?). An optimization problem is a problem with the goal of finding the "best" solution among many (e.g., what is the shortest path from A to B?).
AAP-4.A.3: Efficiency is an estimation of the amount of computational resources used by an algorithm. Efficiency is typically expressed as a function of the size of the input.
AAP-4.A.4: An algorithm's efficiency is determined through formal or mathematical reasoning.
AAP-4.A.5: An algorithm's efficiency can be informally measured by determining the number of times a statement or group of statements executes.
AAP-4.A.6: Different correct algorithms for the same problem can have different efficiencies.
AAP-4.A.7: Algorithms with a polynomial efficiency or slower (constant, linear, square, cube, etc.) are said to run in a reasonable amount of time. Algorithms with exponential or factorial efficiencies are examples of algorithms that run in an unreasonable amount of time.
AAP-4.A.8: Some problems cannot be solved in a reasonable amount of time because there is no efficient algorithm for solving them. In these cases, approximate solutions are sought.
AAP-4.A.9: A heuristic is an approach to a problem that produces a solution that is not guaranteed to be optimal but may be used when techniques that are guaranteed to always find an optimal solution are impractical.
AAP-4.B.1: A decidable problem is a decision problem for which an algorithm can be written to produce a correct output for all inputs (e.g., Is the number even?).
AAP-4.B.2: An undecidable problem is one for which no algorithm can be constructed that is always capable of providing a correct yes-or-no answer.
AAP-4.B.3: An undecidable problem may have some instances that have an algorithmic solution, but there is no algorithmic solution that could solve all instances of the problem.
CSN-2.A.1: Sequential computing is a computational model in which operations are performed in order one at a time.
CSN-2.A.2: Parallel computing is a computational model where the program is broken into multiple smaller sequential computing operations, some of which are performed simultaneously.
CSN-2.A.3: Distributed computing is a computational model in which multiple devices are used to run a program.
CSN-2.A.4: Comparing efficiency of solutions can be done by comparing the time it takes them to perform the same task.
CSN-2.A.5: A sequential solution takes as long as the sum of all of its steps.
CSN-2.A.6: A parallel computing solution takes as long as its sequential tasks plus the longest of its parallel tasks.
CSN-2.A.7: The "speedup" of a parallel solution is measured in the time it took to complete the task sequentially divided by the time it took to complete the task when done in parallel.
CSN-2.B.1: Parallel computing consists of a parallel portion and a sequential portion.
CSN-2.B.2: Solutions that use parallel computing can scale more effectively than solutions that use sequential computing.
CSN-2.B.3: Distributed computing allows problems to be solved that could not be solved on a single computer because of either the processing time or storage needs involved.
CSN-2.B.4: Distributed computing allows much larger problems to be solved quicker than they could be solved using a single computer.
CSN-2.B.5: When increasing the use of parallel computing in a solution, the efficiency of the solution is still limited by the sequential portion. This means that at some point, adding parallel portions will no longer meaningfully increase efficiency.